CONVERTING FROM STANDARD FORM TO FACTORED FORM

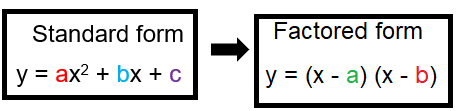
To convert the standard form to factored form, we should know about about how to factorize the quadratic polynomial.

To factorize the quadratic polynomial which is in the form ax² + bx + c, first we will check the coefficient of x^2.

Step 1 :

• If the coefficient of x² is 1, take c and decompose it into two parts.
• If the coefficient of x² is not 1, take ac and decompose it into two parts.

Step 2 :

Such that the product of those two factors is equal to c or ac and the when we combine it we should get the middle term (b).

Step 3 :

Write the middle term as sum of those two factors that we have received from step 2.

Step 4 :

Using grouping, write them as product of factors.

Problem 1 :

Convert f(x) = 3x² + 18x - 48 to factored form.

Solution :

f(x) = 3x² + 18x - 48

Here every term is a multiple of 3. Factoring 3 out.

f(x) = 3(x² + 6x - 16)

-16 = -2⋅8

f(x) = 3(x² -2x + 8x - 16)

f(x) = 3[x(x -2) + 8(x - 2)]

f(x) = 3(x - 2) (x + 8)

Problem 2 :

Factorize 2x² +4x + 2

Solution :

Let f(x) = 2x² +4x + 2

f(x) = 2(x² + 2x + 1)

f(x) = 2(x² + x + x + 1)

f(x) = 2[x(x + 1) + (x + 1)]

f(x) = 2 (x + 1) (x + 1)

Problem 3 :

The height of the foot ball kicked from the ground is given by the function h(t) = -5t² + 20, where h(t) is height in meters and t is the time in seconds from its release.

(i)  Write the function in factored form.

(ii)  When will the foot ball hit the ground ?

Solution :

(i)  h(t) = -5t² + 20

Factoring -5, we get

h(t) = -5(t² - 4)

h(t) = -5(t² - 2²)

t² - 2² looks like a² - b²

The expansion of a² - b² = (a + b)(a - b)

h(t) = -5(t + 2) (t - 2)

(ii)  When it hits the ground, the height will become zero.

0 = -5(t + 2) (t - 2)

Equating each factor to zero, we get

t + 2 = 0 and t - 2 = 0

t = -2 and t = 2

Problem 4 :

Solve x² - 8x + 12 = -3

Move everything to one side and find zeros.

Solution :

x² - 8x + 12 = -3

Add 3 on both sides, we get

x² - 8x + 12 + 3 = 0

x² - 8x + 15 = 0

x² - 3x - 5x + 15 = 0

Using grouping, we get

x(x - 3) - 5(x - 3) = 0

(x - 5)(x - 3) = 0

Equating each factor to zero, we get

x - 5  = 0 and x - 3 = 0

x = 5 and x = 3

Problem 5 :

Find the points of intersections of the graphs

f(x) = x² - 8x + 12 and g(x) = -3

Solution :

f(x) = x² - 8x + 12 -----(1)

g(x) = -3 -----(2)

(1) = (2)

x² - 8x + 12 = -3

Add 3 on both sides on both sides.

x² - 8x + 12 + 3 = 0

x² - 8x + 15 = 0

x² - 3x - 5x + 15 = 0

Using grouping, we get

x(x - 3) - 5(x - 3) = 0

(x - 5)(x - 3) = 0

Equating each factor to zero, we get

x = 5 and x = 3

So, points of intersections are (5, -3) and (3, -3).

Problem 6 :

The path a dolphin travels when it rises above the ocean’s surface can be modelled by the function 

h(d) = -0.2d² + 2d

where h(d) is the height of the dolphin above the water’s surface and d is the horizontal distance from the point where the dolphin broke the water’s surface, both in feet. When will the dolphin reach a height of 1.8 feet? 

Solution :

h(d) = -0.2d² + 2d

When h(d) = 1.8

1.8 = -0.2d² + 2d

-0.2d² + 2d = 1.8

-0.2d² + 2d - 1.8 = 0

Multiply the equation by -10, we get

2d² + 20d + 18 = 0

Dividing by 2, we get

d² - 10d + 9 = 0

(d - 1) (d - 9) = 0

Equating each factor to zero.

d - 1 = 0 and d - 9 = 0

d = 1 and d = 9

So, at d = 1 and d = 9 the dolphin will reach the height 200 m.