CONVERTING FROM VERTEX FORM TO STANDARD FORM

To convert standard form to vertex form, we may follow the different ways.

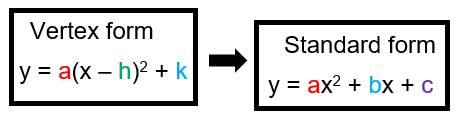
We should aware of the following algebraic identities.

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²

Convert the following quadratics from vertex form to standard form.

Problem 1 :

y = -(x – 1)² – 1

Solution :

y = -(x – 1)² – 1

Using the algebraic identity, we can expand this and then distribute the negative sign.

(x – 1)² = x² - 2x(1) + 1²

(x – 1)² = x² - 2x + 1

y = -(x² - 2x + 1) – 1

Distributing the negative, we get

y = -x² + 2x - 1 – 1

y = -x² + 2x - 2

Problem 2 :

y = 2(x – 2)² – 3

Solution :

y = 2(x – 2)² – 3

Using the algebraic identity, we can expand it and multiply by 2.

(x – 2)² = x² - 2x(2) + 2²

(x – 2)² = x² - 4x + 4

y = 2(x² - 4x + 4) – 3

Distributing 2, we get

y = 2x² - 8x + 8 – 3

Combining the like terms, we get

y = 2x² - 8x + 5

Problem 3 :

y = (x + 4)² + 4

Solution :

y = (x + 4)² + 4

Using the algebraic identity, we can expand it and multiply by 2.

(x + 4)² = x² - 2x(4) + 4²

(x – 1)² = x² - 8x + 16

y = (x² - 8x + 16) + 4

Combining the like terms, we get

y = x² - 8x + 20

Problem 4 :

y = (1/2)(x - 2)² - 4

Solution :

y = (1/2)(x - 2)² - 4

Using the algebraic identity, we can expand it and multiply by 2.

(x - 2)² = x² - 2x(2) + 2²

(x – 2)² = x² - 4x + 4

y = (1/2)(x² - 4x + 4) - 4

Distributing 1/2, we get

y = (1/2)x² - 2x + 2 - 4

y = (1/2)x² - 2x - 2

Problem 5 :

For the function y = (x - 2)² - 1

a) State the coordinates of x and y intercepts

b) State the axis of symmetry

c) Determine the turnining point of the function and state whether it's a maximum or minimum function.

Solution :

y = (x - 2)² - 1

a) x-intercept :

Put y = 0

(x - 2)² - 1 = 0

(x - 2)² = 1

x - 2 = √1

x - 2 = ±1

x - 2 = 1 and x -2 = -1

x = 1 + 2 and x = -1 + 2

x = 3 and x = 1

x-intercepts are (3, 0) and (1, 0)

y-intercept :

Put x = 0

y = (0 - 2)² - 1

= 4 - 1

y = 3

So, the y-intercept is (0, 3).

b) Since the given quadratic function is in the vertex form, we can find the vertex by comparing the given function with vertex form.

 y = (x - 2)² - 1

 y = (x - h)² + k

Here (h, k) is (2, -1)

So, the vertex is (2, -1).

c) y = (x - 2)² - 1

Since the parabola opens up, it must have minimum and minimum is at x = 2 and the minimum value is y = -1.

Problem 6 :

The figure below shows the part of the graph of quadratic function y = ax² + 4x + c

a) Write the value of c.

b)  Find the value of a

c)  Write the quadratic function in factored form.

Solution :

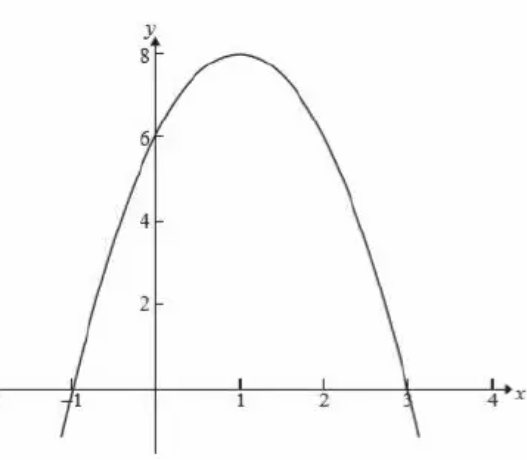
y = ax² + 4x + c

x-intercepts are -1 and 3.

x = -1 and x = 3

Writing the solutions in factored form, we get

(x + 1)(x - 3) = 0

x² - 3x + 1x - 3 = 0

x² - 2x - 3 = 0

a)

The required quadratic function represented in the graph will be y = k(x² - 2x - 3). To find the value of k, we have to apply the point (0, 6).

y = k(x² - 2x - 3)

6 = k(0² - 2(0) - 3)

6 = k(-3)

k = -2

y = -2(x² - 2x - 3)

y = -2x² + 4x + 6

So, the values of a and c are -2 and 6 respectively.

c) Factroed form :

y = -2x² + 4x + 6

y = -2(x² - 2x - 3)

y= -2(x - 3)(x + 1)

Problem 7 :

The y-intercept point for the graph of y = x² + x - 3 is above the x-axis.

Solution :

y = x² + x - 3

To find y-intercept for the graph of quadratic polynomial, we have to apply x= 0

y = 0² + 0 - 3

y = -3

The y-intercept is (0, -3). Then the y-intercept of the parabola is below the x-axis. The given statement is false.

Problem 8 :

The maximum value of f(x) = 15 - 2x - x² is 12.

Solution :

f(x) = 15 - 2x - x²

f(x) = - (x² + 2x - 15)

To find maximum or minimum value of the quadratic function, we should write it in the vertex form.

= - [x² + 2x(1) + 1² - 1² - 15]

= - [(x + 1)² - 1² - 15]

= - [(x + 1)² - 16]

y = -(x + 1)² + 16

y = -(x - h)² + k

The parabola opens down, it must have maximum at x = -1 and maximum value is 16. But the given value is 12. So, the statement is false.