FINDING ANGLE MEASURES BETWEEN INTERSECTING LINES WORKSHEET

Problem 1 :

Solution

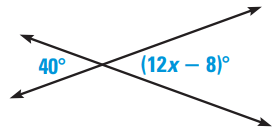
Problem 2 :

Find the missing angles.

Solution

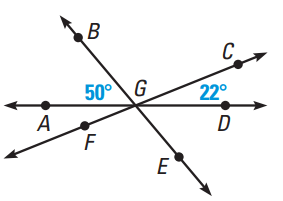
Problem 3 :

Solve for w.

Solution

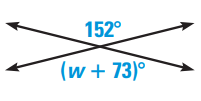
Problem 4 :

Solve for n.

Solution

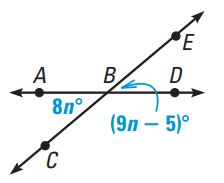
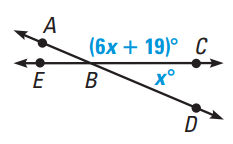
Problem 5 :

Solve for x.

Solution

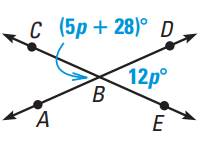
Problem 6 :

Solve for p.

Solution

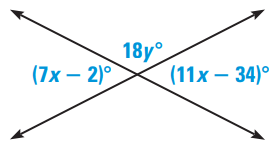
Problem 7 :

Solve for x.

Solution

Problem 8 :

Solve for x.

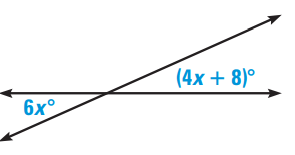
a. Use the Vertical Angles Theorem to write an equation.

b. Solve your equation to find the value of x.

c. Find the measures of the acute angles formed by the lines.

d. Find the measures of the obtuse angles formed by the lines.

Solution

Problem 9 :

The measures of two complementary angles have a ratio of 3:2. What is the measure of the larger angle?

Solution

Problem 10 :

Write and solve a system of equations to fi nd the values of x and y

Solution

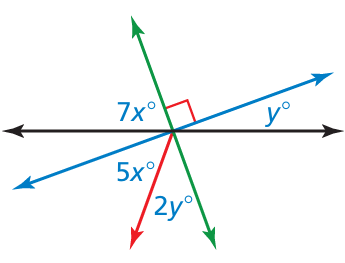
Problem 11 :

Two angles form a linear pair. The measure of one angle is twice the measure of the other angle. Find the angles.

Solution

Problem 1 :

Angles G and H are complementary. If m∠G = 3x + 6 and m∠H = 2x - 11. what is the measure of each angle?

Solution

Problem 2 :

The measures of angles A and B are supplementary. What is the measure of each angle?

Solution

Problem 3 :

An angle is five its supplement. Find both angles.

Solution

Problem 4 :

An angle is 74 degrees more than its complement. Find both angles.

Solution

Problem 5 :

The supplement of an angle exceeds the angle by 60 degrees. Find both angles.

Solution

Problem 6 :

Find the number of degrees in an angle which is 42 less than its complement.

Solution

Problem 7 :

Find the number of degrees in an angle which is 120 less than its supplement.   

Solution

Problem 8 :

The complement of an angle is 30 less than twice the angle. Find the larger angle.

Solution

Problem 9 :

Angles A and B are complementary. If m∠A = 3x - 8 and m∠B = 5x + 10, what is the measure of each angle?

Solution

Problem 10 :

Angles Q and R are supplementary. If m∠Q = 4x + 9 and m∠R = 8x + 3, what is the measure of each angle?

Solution

Problem 1 :

Solution

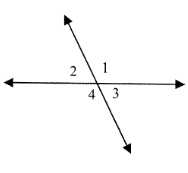
Problem 2 :

From the picture at the right, name the 2 sets of vertical angles?

Solution

Problem 3 :

Vertical angles are always ________.

Solution

Problem 4 :

Linear pairs are always _____, which means they add up to _____.

Solution

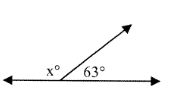
Problem 5 :

x = _____

Solution

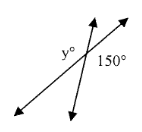
Problem 6 :

y = _____

Solution

Problem 8 :

a = _____

Solution

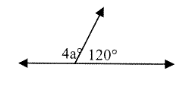
Problem 9 :

w = _____

Solution

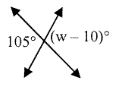
Problem 10 :

d = _____

Solution

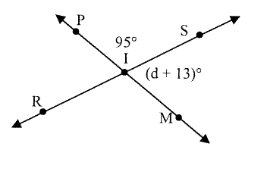
Tell whether the statement is always, sometimes, or never true. Explain your reasoning.

Problem 11 :

Complementary angles are adjacent.

Solution

Problem 12 :

Angles in a linear pair are supplements of each other.

Solution

Problem 13 :

Vertical angles are adjacent.

Solution

Problem 14 :

Vertical angles are supplements of each other.

Solution

Problem 15 :

If an angle is acute, then its complement is greater than its supplement.

Solution

Problem 16 :

If two complementary angles are congruent, then the measure of each angle is 45°. 

Solution

Problem 17 :

Explain why the supplement of an acute angle must be obtuse. 

Solution

Problem 18 :

Explain why an obtuse angle does not have a complement.

Solution

Problem 19 :

The iron cross is a skiing trick in which the tips of the skis are crossed while the skier is airborne. Find the value of x in the iron cross shown.

Solution

Problem 20 :

The measure of an angle is 9 more than twice its complement. 

Solution

Problem 21 :

Two angles form a linear pair. The measure of one angle is four times the measure of the other angle.

Solution

Related Pages

• Parallel lines and transversal worksheet
• Angle relationships with parallel lines
• Complementary and supplementary angles worksheet
  
• How to find the area of a triangle
  
• Find the missing side of a right triangle worksheet