FIND THE MISSING SIDE OF A RIGHT TRIANGLE WORKSHEET

Find x.

Problem 1 :

Solution

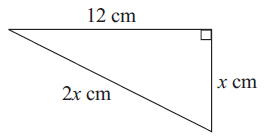
Problem 2 :

Solution

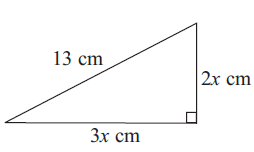
Problem 3 :

Solution

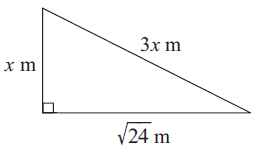
Problem 4 :

Solution

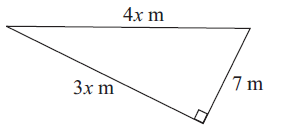
Problem 5 :

Solution

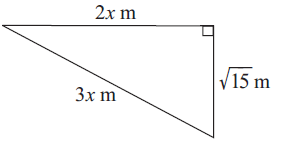
Problem 6 :

Solution

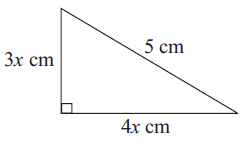
Problem 7 :

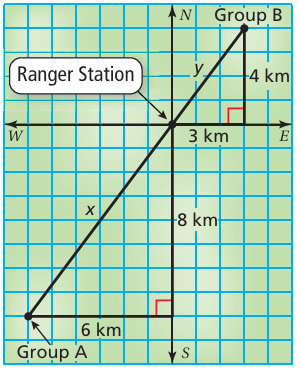
Hiking Group A leaves a ranger station and hikes 8 kilometers south then 6 kilometers west. Group B leaves the station and hikes 3 kilometers east then 4 kilometers north. Using the fi gure, how far apart are the two groups of hikers?

a) 5 km     b)  10 km    c)  15 km    d)  21 km

Solution

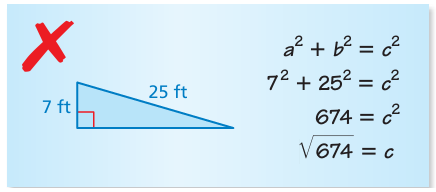
Problem 8 :

Describe and correct the error in fi nding the missing length of the triangle.

Solution

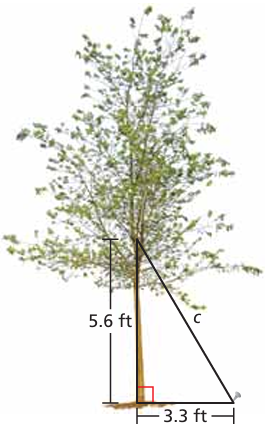
Problem 9 :

How long is the wire that supports the tree?

Solution

Find the value of x.

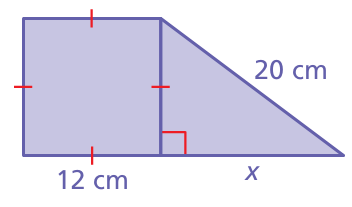
Problem 10 :

Solution

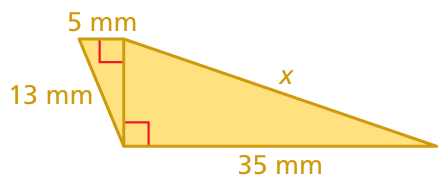
Problem 11 :

Solution

Problem 12 :

Solution

Problem 13 :

Televisions are advertised by the lengths of their diagonals. A store has a sale on televisions 40 inches and larger. Is the television on sale? Explain.

Solution

Problem 1 :

A rectangle has sides of length 7 cm and 3 cm. Find the length of its diagonals.                 Solution

Problem 2 :

The longer side of the rectangle is double the length of the shorter side. If the length of a diagonal is 10 cm, find the dimension of the rectangle.          Solution

Problem 3 :

A rectangle with diagonals of length 30 cm has sides in the ratio 3 : 1. Find the 

(a) Perimeter   (b) Area of the rectangle.          Solution

Problem 4 :

A rhombus has sides of length 7 cm. One of the diagonals is 10 cm long. Find the length of the other diagonal.

Solution

Problem 5 :

A square has diagonals of length 8 cm. Find the length of the sides.                  Solution

Problem 6 :

A rhombus has diagonal of length 4 cm and 6 cm. Find the perimeter.                      Solution

Problem 7 :

An equilateral triangle has sides of 6 cm

(a)  Find the length one of its altitude.

(b)  Find the area of the triangle.

Solution

Problem 8 :

An isosceles triangle has equal sides of length 8 cm and the base of length 6 cm.

(a)  Find the altitude of the triangle

(b)  Find the area of the triangle

Solution

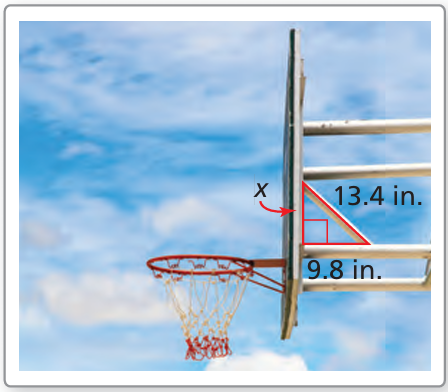
Problem 9 :

The backboard of the basketball hoop forms a right triangle with the supporting rods, as shown. Use the Pythagorean Theorem to approximate the distance between the rods where they meet the backboard.

Solution

Problem 10 :

The fire escape forms a right triangle, as shown. Find the distance between the two platforms.

Solution

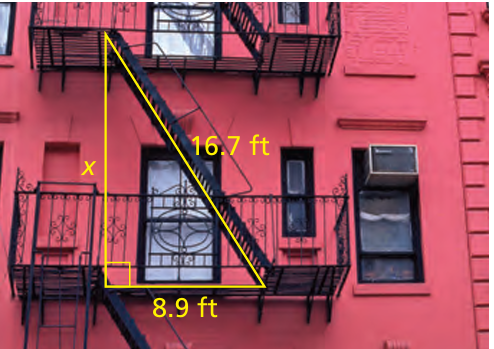
Problem 11 :

Approximate the wingspan of the butterfly.

Solution

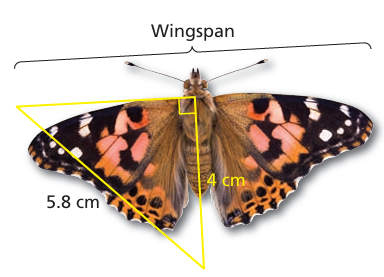
Problem 12 :

The legs of a right triangle have lengths of 28 meters and 21 meters. The hypotenuse has a length of 5x meters. What is the value of x ?

Solution

Problem 1 :

A land surveyor uses this diagram to find x, find the length of lake.

Solution

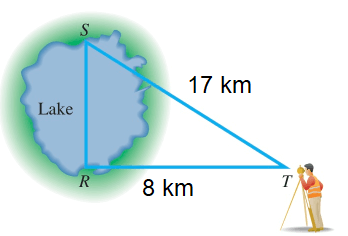
Problem 2 :

A foot ladder leans against a shed reaching a height of x feet. The base of the ladder is 10 feet from the shed.

Solution

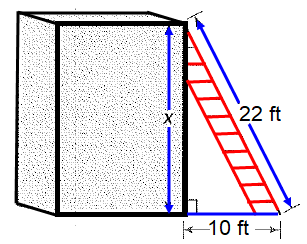
Problem 3 :

The diagram shows a sailboat. What is approximate area of the sail shown ?

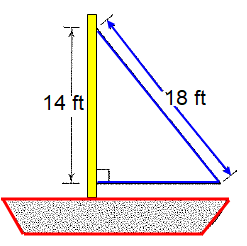
(a)  79 square feet     (b)  126 square feet

(c)  158 square feet      (d)  200 square feet

Solution

Problem 4 :

The television screen has a 25 inch diagonal and a 15 inch height. What is the area of the screen ?

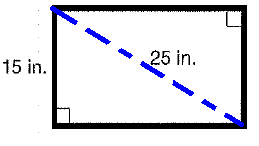
(a)  150 square inches    (b)  300 square inches

(c)  375 square inches   (d) 437 square inches

Solution

Problem 5 :

If two forces, A and B pull at right angles from each other, the resultant force can be represented as the diagonal of a rectangle.

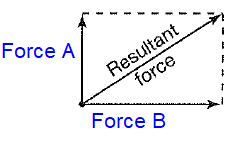
If a 21 pound force and a 28 pound force are pulling of an object, and the resultant force is 35 pounds, are the forces pulling a right angles ?

Solution

Problem 6 :

The distance across a pond cannot be directly measured. A land surveyor takes some other measurements and uses them to find d, the distance across the pond.

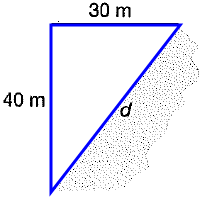
What is the distance across the pond ?

(a)  70 meters   (b) 35 meters   (c)  50 meters    (d) 10 meters

Solution

Problem 7 :

The solid line below show the route Maddy's bus takes to school. The dashed line shows a shortcut she takes through the park when she rides her bike to school. What is the difference in km between the shortcut and the usual route ?

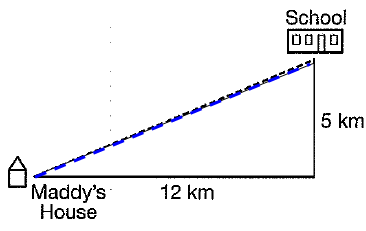
(a)  10 km     (b)  4 km     (c)  7 km    (d)  3 km

Solution

Problem 8 :

On the map below, the post office is at origin (0, 0) and each unit represents 1 km. Amy lives 6 km east and 8 km north of the post office. if she rides her bike directly from her house to the post office, how far will she ride her bike ?

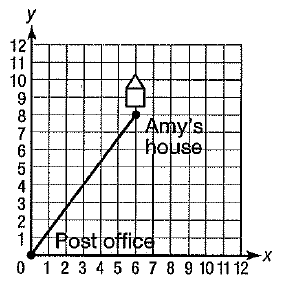
(a)  4.8 km   (b)  12 km   (c)  10 km   (d)  14 km

Solution