FIND THE LENGTH OF A MISSING SIDE OF A RIGHT TRIAGLE

In a right angled triangle, with hypotenuse c and legs a and b.

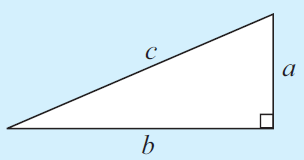
c² = a² + b²

Note :

The hypotenuse is always the longest side and it is opposite the right angle.

• If we know the lengths of any two sides of the triangle then we can calculate the length of the third side.
• If we know the lengths of three sides then we can determine whether it is a right triangle or not.

Find x.

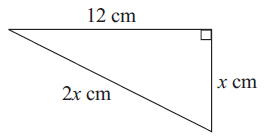
Problem 1 :

Solution :

The side which is opposite to right angle is 2x.

Hypotenuse = 2x

Using Pythagorean theorem :

(2x)² = 12² + x²

4x² = 144 + x²

Subtract x² on both sides, we get

3x² = 144

Divide by 3 on both sides, we get

x² = 144/3

x² = 48

x = √48

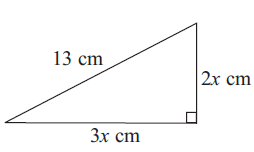
Problem 2 :

Solution :

The side which is opposite to right angle is 13.

Hypotenuse = 13

Using Pythagorean theorem :

(13)² = (3x)² + (2x)²

169 = 9x² + 4x²

169 = 13x²

x² = 169/13

x² = 13

x = √13

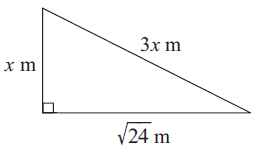
Problem 3 :

Solution :

The side which is opposite to right angle is 3x.

Hypotenuse = 3x

Using Pythagorean theorem :

(3x)² = x² + (√24)²

9x² = x² + 24

Subtracting x² on both sides, we get

8x² = 24

Dividing by 8 on both sides, we get

x² = 3

x = √3

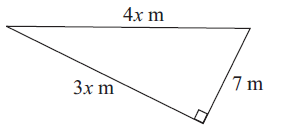
Problem 4 :

Solution :

The side which is opposite to right angle is 4x.

Hypotenuse = 4x

Using Pythagorean theorem :

(4x)² = (3x)² + 7²

16x² = 9x² + 49

Subtracting 9x² on both sides.

7x² = 49

Dividing by 7 on both sides, we get

x² = 49/7

x² = 7

x = √7

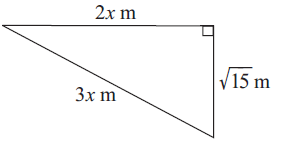
Problem 5 :

Solution :

The side which is opposite to right angle is 3x.

Hypotenuse = 3x

Using Pythagorean theorem :

(3x)² = (2x)² + √15²

9x² = 4x² + 15

Subtracting 4x² on both sides.

5x² = 15

Dividing by 5 on both sides, we get

x² = 15/5

x² = 3

x = √3

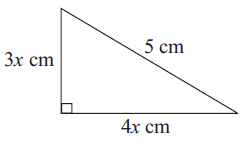
Problem 6 :

Solution :

The side which is opposite to right angle is 5.

Hypotenuse = 5

Using Pythagorean theorem :

5² = (3x)² + (4x)²

25 = 9x² + 16x²

25 = 25x²

x² = 1

x = 1

Problem 7 :

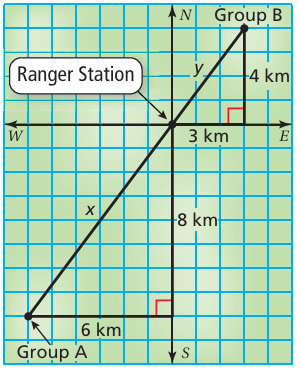
Hiking Group A leaves a ranger station and hikes 8 kilometers south then 6 kilometers west. Group B leaves the station and hikes 3 kilometers east then 4 kilometers north. Using the fi gure, how far apart are the two groups of hikers?

a) 5 km     b)  10 km    c)  15 km    d)  21 km

Solution :

Distance covered by Group A :

x² = 6² + 8²

x² = 36 + 64

x² = 100

x = 10

Distance covered by Group A is 10 km.

Distance covered by Group B :

x² = 3² + 4²

x² = 9 + 16

x² = 25

x = 5

Distance covered by Group B is 5 km.

Ttoal distance covered by two groups = 10 + 5

= 15 km

So, total distance covered by two groups is 15 km. Option c is correct.

Problem 8 :

Describe and correct the error in fi nding the missing length of the triangle.

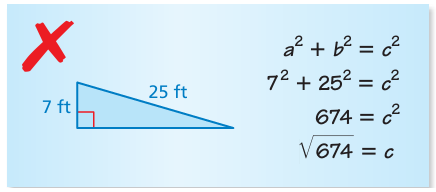
Solution :

In any right triangle,

the square of hypotenuse is equal to sum of squares of remaining sides.

The error is the concept itself.

Let x be the missing side.

25² = x² + 7²

625 = x² + 49

x² = 625 - 49

x² = 576

x = 24 ft

Problem 9 :

How long is the wire that supports the tree?

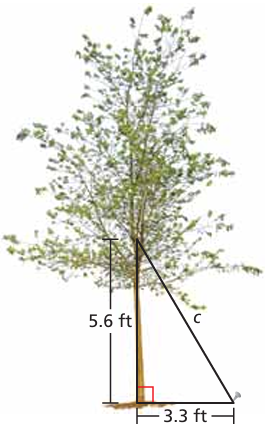
Solution :

Given that c is the missing side.

5.6² + 3.3² = c²

31.36 + 10.89 = c²

42.25 = c²

c = √42.25

c = 6.5

The length of the wire is 6.5 ft.

Find the value of x.

Problem 10 :

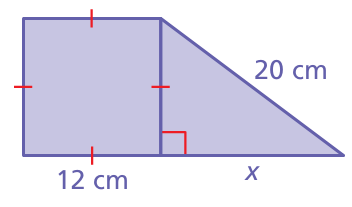
Solution :

We have square and triangle, in the triangle using pythagorean theorem

20² = 12² + x²

400 = 144 + x²

x² = 400 - 144

x² = 256

x = √256

x = 16 cm

So, the missing side is 16 cm.

Problem 11 :

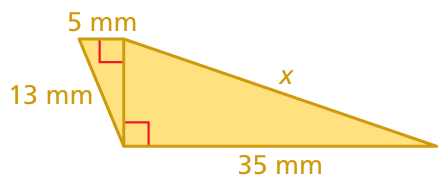
Solution :

We have two triangles. The triangle at the left. Let h be the height of the triangle.

13² = 5² + h²

169 = 25 + h²

h² = 169 - 25

h² = 144

h = √144

h = 12 mm

In the triangle to the right,

h² + 35² = x²

Applying the value of h, we get

12² + 35² = x²

144 + 1225 = x²

x² = 1369

x = √1369

x = 17 mm

So, the missing side is 17 mm.

Problem 12 :

Solution :

The drawn line is a perpendicular bisector.

In the triangle right,

10² = 8² + h²

100 - 64 = h²

h² = 36

h = √36

h = 6 ft

In the triangle to the left,

x² = 8² + 6²

x² = 64 + 36

x² = 100

x = √100

x = 10 ft

So, the missing side is 10 ft.

Problem 13 :

Televisions are advertised by the lengths of their diagonals. A store has a sale on televisions 40 inches and larger. Is the television on sale? Explain.

Solution :

d² = 24² + 32²

d² = 576 + 1024

d² = 1600

d = √40 x 40

d = 40 inches

Yes the television is on the sale.