PARALLEL LINES AND TRANSVERSAL WORKSHEET

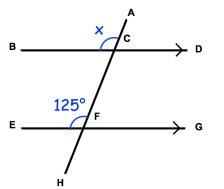
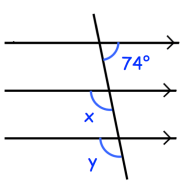
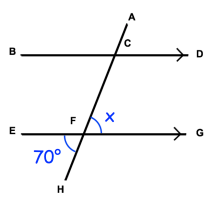
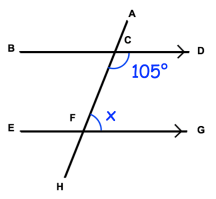
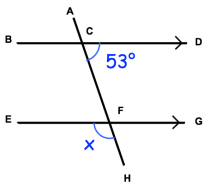
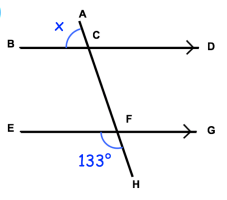
Find the angle x in the figure given below. Give your reason.

(1)

(2)

(3)

(4)

(5)

(6)

Problem 7 :

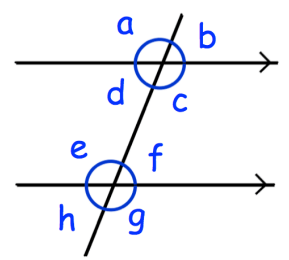
(a) Which angle is corresponding to angle c?

(b) Which angle is alternate to angle d?

(d) Which angle is vertically opposite to angle a?

(e) Which angle is alternate to angle e?

(f) Which angle is co-interior with angle c?

(g) Which angle is vertically opposite to angle h?

(h) Which angle is co-interior with angle e?

(i) Which angle is corresponding to angle a?

(j) Which angle is vertically opposite to angle g?

Solution

Problem 8 :

Find the value of the variable(s) in each figure. Explain your reasoning.

Solution

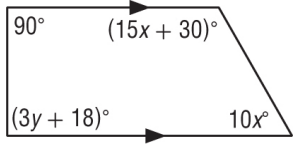
Problem 9 :

Find the value of the variable(s) in each figure. Explain your reasoning.

Solution

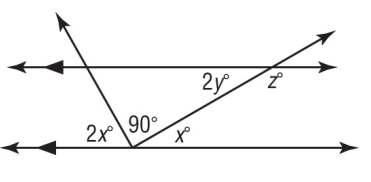
Problem 10 :

(Using a 3rd parallel Line – Auxilury Line)

Solution

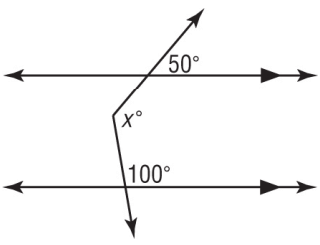
Example 11 :

Use the figure to find the measures of the numbered angles. Explain your reasoning.

Solution

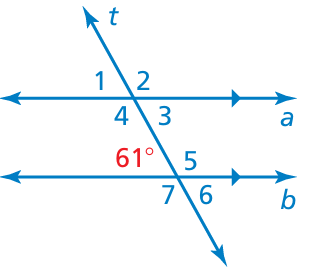
Example 12 :

Use the figure to find the measures of the numbered angles. Explain your reasoning

Solution

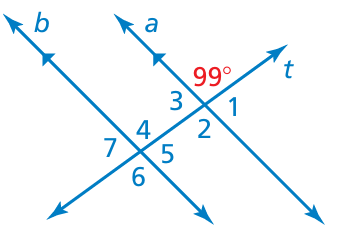
Example 13 :

Use the figure to find the measures of the numbered angles. Explain your reasoning

Solution

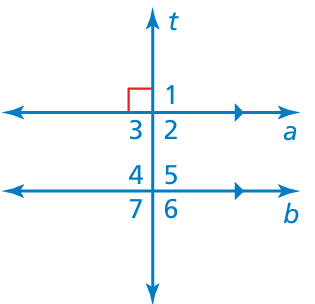
Answer

1) x = 125

2) x = 57

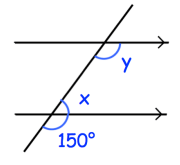
3) x = 30 and y = 150

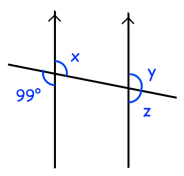
4) x = 81, y = 81 and z = 99

5) x = 106 and y = 106

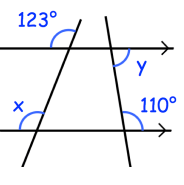
6) x = 123 and y = 70

(a) Corresponding angle of ∠c is ∠f.

(b) ∠d and ∠f are alternate angles.

(d) Vertically opposite to ∠a is ∠c.

(e) Alternate angle of ∠e is ∠c.

(f) The co-interior ∠c is ∠f.

(g) Vertically opposite to ∠h is ∠f.

(h) Co-interior angle with ∠e is ∠d.

(i) Corresponding to ∠a is ∠e.

(j) Vertically opposite to ∠g is ∠e.

8) x = 6 and y = 24

9) x = 30, y = 15 and z = 150

10) x = 130

11)

∠1 = 61

∠4 and 61 are co-interior angles. Then, their sum is 180 degree.

∠4 + 61 = 180

∠4 = 180 - 61

∠4 = 119

∠2 = ∠4 (vertical angles)

∠2 = 119

∠1 = ∠3 (vertical angles)

∠3 = 61

∠6 = 61 (Vertical angles)

∠4 = ∠7 (Corresponding angles)

∠7 = 119

∠5 = 119 (vertical angles)

12)

∠1 + 99 = 180

∠1 = 180 - 99

∠1 = 81

∠3 = 81 (vertical angles)

∠1 = ∠5 = 81 (Corresponding angles)

∠2 = 99 (vertical angles)

∠2 = ∠6 = 99 (Corresponding angles)

∠7 = 81

∠4 = 99 (Corresponding angles)

13)

∠1 = 90

∠2 = 90 (vertical angles)

∠3 = 90 (corresponding angles)

∠4 = ∠5 = ∠6 = ∠7 = 90 degree

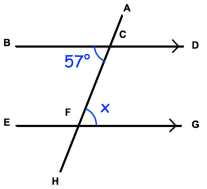
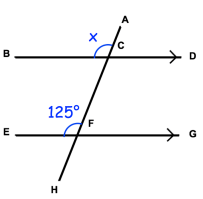
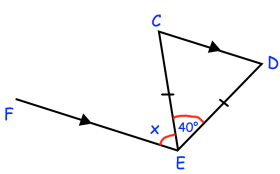
Find the angle x in the figure given below. Give your reason.

(1)

(2)

(3)

(4)

(5)

(6)

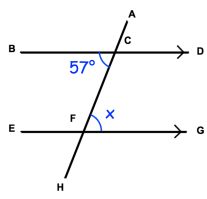
Problem 7 :

Are the lines AB and CD parallel? Explain your answer.

Solution

Example 8 :

Find the missing angle. Give reasons for your answer

Solution

Problem 9 :

Find x.

Solution

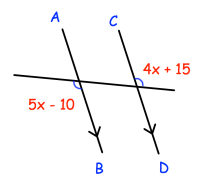
Problem 10 :

Find x.

Solution

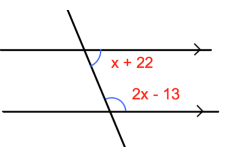
Problem 11 :

A store owner uses pieces of tape to paint a window advertisement. The letters are slanted at an 80° angle. What is the measure of ∠1?

a) 80° b) 100° c) 110° d) 120°

Solution

Problem 12 :

The photo shows a portion of the St. Petersburg-Clearwater International Airport. Describe the relationship between each pair of angles.

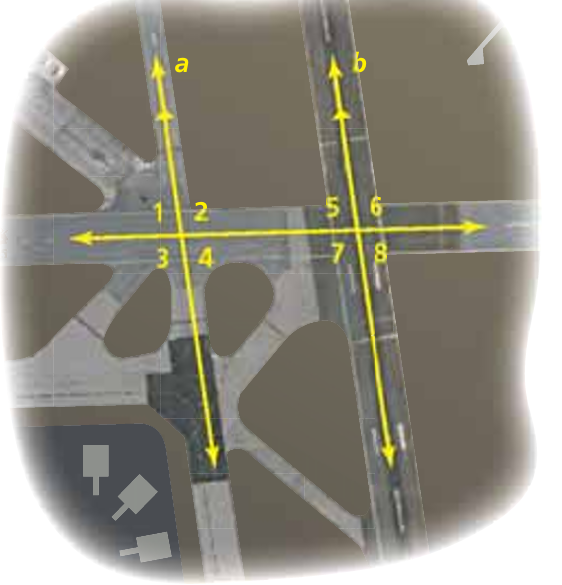
a. ∠3 and ∠6

a. ∠2 and ∠7

Solution

Problem 13 :

Describe and correct the error in describing the relationship between the angles.

Solution

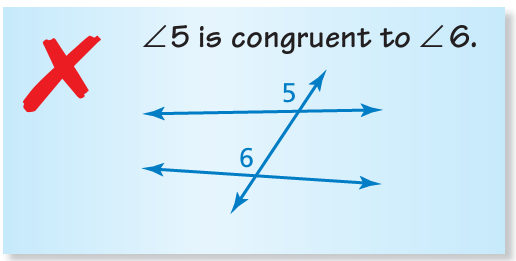
Problem 14 :

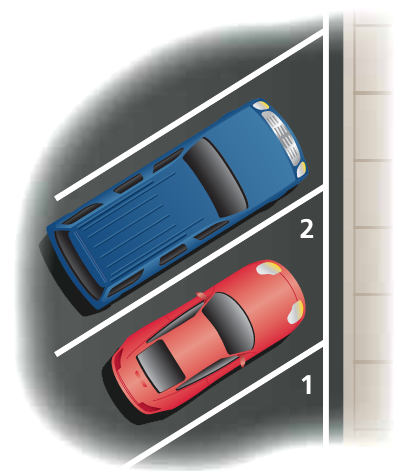
The painted lines that separate parking spaces are parallel. The measure of ∠1 is 60°. What is the measure of ∠2? Explain.

Solution

Problem 15 :

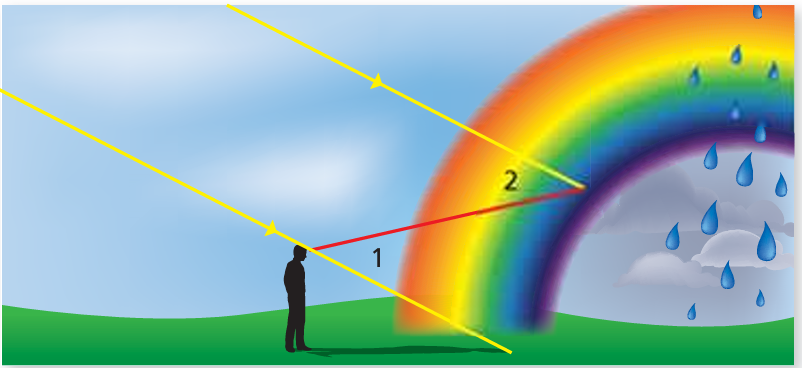
A rainbow is formed when sunlight reflects off raindrops at different angles. For blue light, the measure of ∠2 is 40°. What is the measure of ∠1?

Solution

Problem 16 :

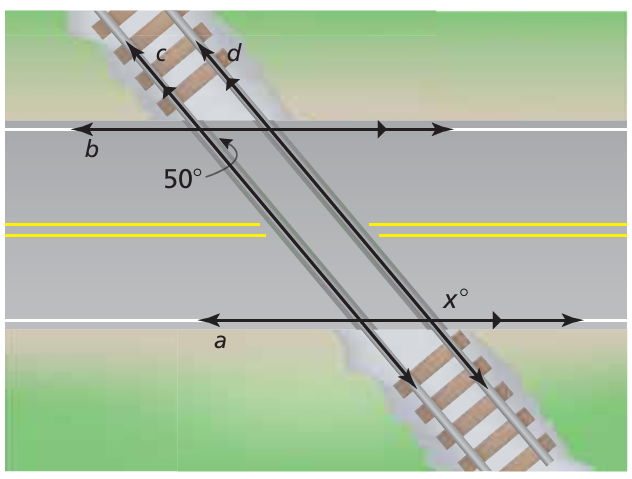
Find the value of x.

Solution

Problem 17 :

Find the value of x.

Solution

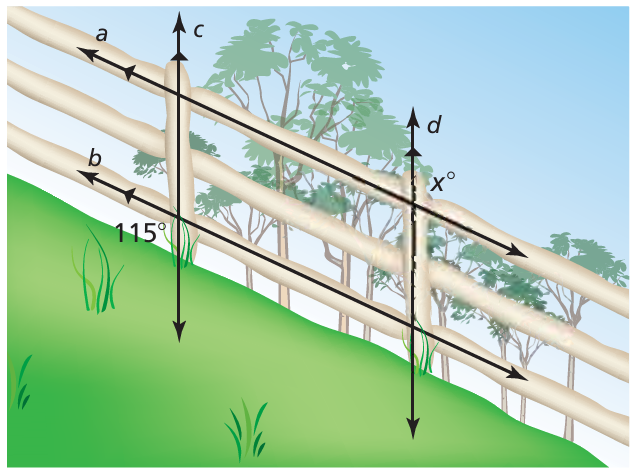
Problem 18 :

The figure shows the angles used to make a double bank shot in an air hockey game

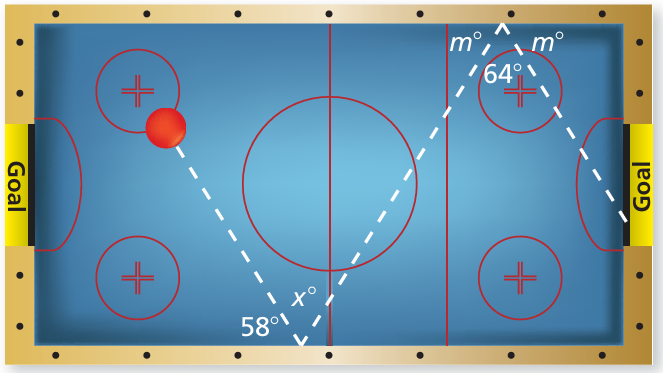
a. Find the value of x.

b. Can you still get the red puck in the goal if x is increased by a little? by a lot? Explain.

Solution

Problem 19 :

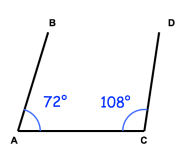
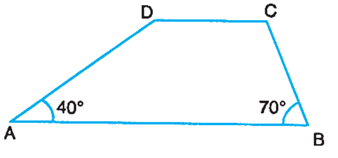
In Figure, ABCD is a trapezium such that AB||DC. Find ∠D and ∠C and verify that sum of the four angles is 360o

Solution

Answers

1) x = 125

2) x = 57

3) x = 70

4) x = 75

5) x = 127

6) x = 47

7) 180

8) x = 70 (Alternate interior angles)

9) x = 25

10) x = 57

11) 100°

12) a) ∠3 and ∠6 are alternate extrior angles.

b) ∠2 and ∠7 are alternate interior angles.

13)

Describing the error :

Since we have no evidence that the lines are parallel, then these two angles may not be equal.

14) ∠1 and ∠2 are corresponding angles.

15) ∠1 = 40

16) x = 130

17) x = 115 degree.

18) a) x = 64

b) Yes, you can still get the red puck in the goal if x is increased by a little, but not if it's increased by a lot

19) ∠D = 140 and ∠C = 110

PARALLEL LINES AND TRANSVERSAL WORKSHEET

Answer

Answers

Recent Articles

Finding Range of Values Inequality Problems

Solving Two Step Inequality Word Problems

Exponential Function Context and Data Modeling