FIND THE MISSING ANGLES WITH TRANSVERSAL

Find the angle x in the figure given below. Give your reason.

Example 1 :

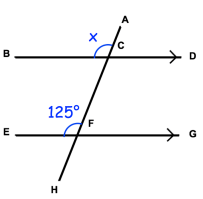
Solution :

∠ACB = ∠CFE

Because they are corresponding angles.

So,

x = 125

Example 2 :

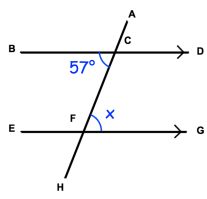
Solution :

∠BCF = ∠CFG

Because they are alternate angles.

So,

x = 57

Example 3 :

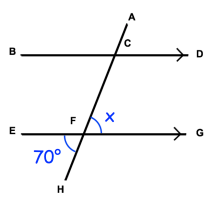
Solution :

∠EFH = ∠CFG

Because they are vertically opposite angles.

So,

x = 70

Example 4 :

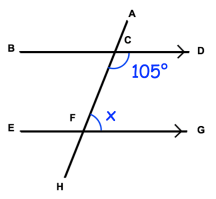
Solution :

∠DCH = ∠CFG

Sum of consecutive interior angle is 180.

x + 105 = 180

x = 180 - 105

x = 75

Example 5 :

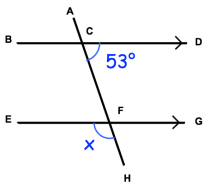
Solution :

∠DCF = ∠EFH

∠DCF = 53

∠CFE + ∠EFH = 180 

53 + x = 180

x = 180 - 53

x = 127

Example 6 :

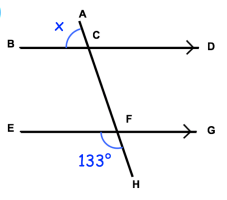
Solution :

∠BCA = ∠DCF (Vertically opposite angles)

∠CFG = ∠EFH (Vertically opposite angles)

∠EFA = ∠BCA = x (Corresponding angles)

∠HFE + ∠EFA = 180

133 + x = 180

x = 180 - 133

x = 47

Example 7 :

Are the lines AB and CD parallel? Explain your answer. 

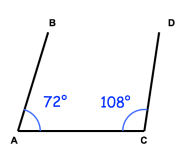
Solution :

By adding the interior angles ,

= ∠BAC + ∠DCA

= 72 + 108

= 180

The sum of interior angles is 180 degree, the angles involving here are parallel.

Example 8 :

Find the missing angle. Give reasons for your answer

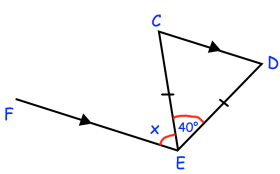
Solution :

Triangle ECD is isosceles triangle.

∠CED + ∠EDC + ∠DCE = 180

∠EDC = ∠DCE

40 + ∠EDC + ∠EDC = 180

Subtract 40 on both sides.

2∠EDC = 180 - 40

2∠EDC = 140

Divide by 2 on both sides.

∠EDC = 70

∠ECD = 70

∠CEF = x

x = 70 (Alternate interior angles)

Example 9 :

Find x.

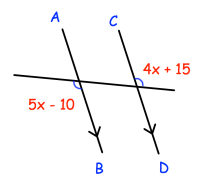
Solution :

5x - 10 = 4x + 15

(Alternate exterior angles)

Subtract 4x on both sides.

5x - 4x - 10 = 15

Add 10 on both sides.

x = 15 + 10

x = 25

Example 10 :

Find x.

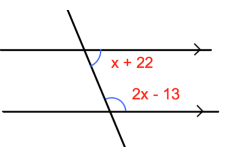
Solution :

The angles involving in the problem given above is consecutive interior angles on the same side of the transversal.

x + 22 + 2x - 13  =  180

3x + 9 = 180

3x = 180 - 9

3x = 171

x = 171/3

x = 57

Example 11 :

A store owner uses pieces of tape to paint a window advertisement. The letters are slanted at an 80° angle. What is the measure of ∠1?

a) 80°     b) 100°     c) 110°      d)  120°

Solution :Solution :

Because all of the letters are slanted at an 80° angle, the dashed lines are parallel. The piece of tape is the transversal. Using the corresponding angles, the 80° angle is congruent to the angle that is supplementary to ∠1.

The measure of ∠1 is 180° − 80° = 100°. The correct answer is b.

Example 12 :

The photo shows a portion of the St. Petersburg-Clearwater International Airport. Describe the relationship between each pair of angles.

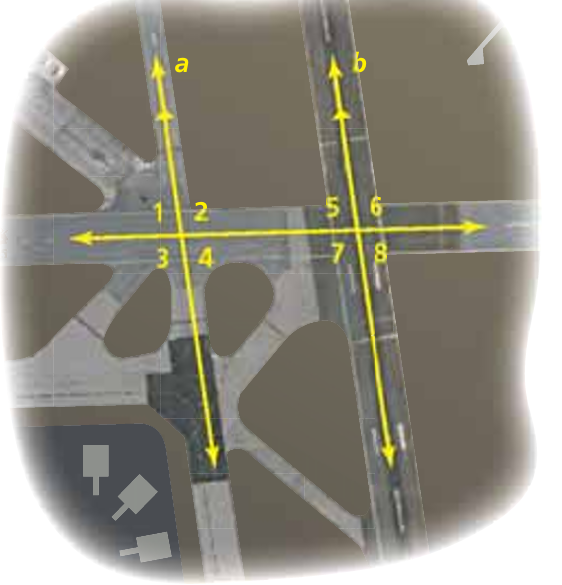
a. ∠3 and ∠6

a. ∠2 and ∠7

Solution :

a. ∠3 and ∠6

∠3 and ∠6 are alternate extrior angles.

a. ∠2 and ∠7

∠2 and ∠7 are alternate interior angles.

Example 13 :

Describe and correct the error in describing the relationship between the angles.

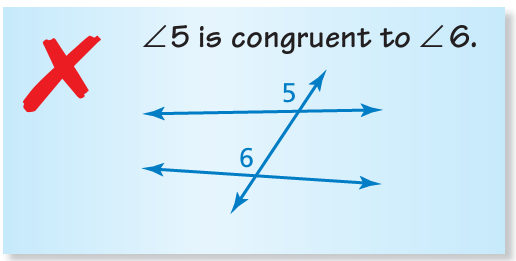
Solution :

Given that ∠5 and ∠6 are congruent.

Describing the error :

Since we have no evidence that the lines are parallel, then these two angles may not be equal. 

Example 14 :

The painted lines that separate parking spaces are parallel. The measure of ∠1 is 60°. What is the measure of ∠2? Explain.

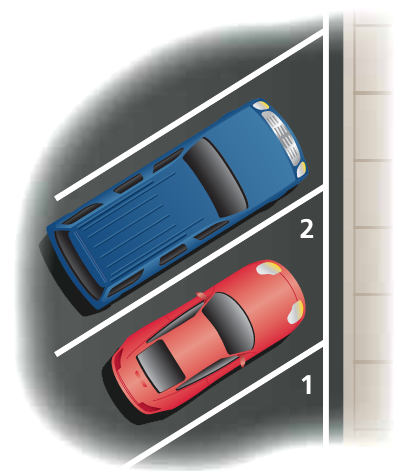
Solution :

We have the information that the lines are parallel. ∠1 and ∠2 are corresponding angles.

Example 15 :

A rainbow is formed when sunlight reflects off raindrops at different angles. For blue light, the measure of ∠2 is 40°. What is the measure of ∠1?

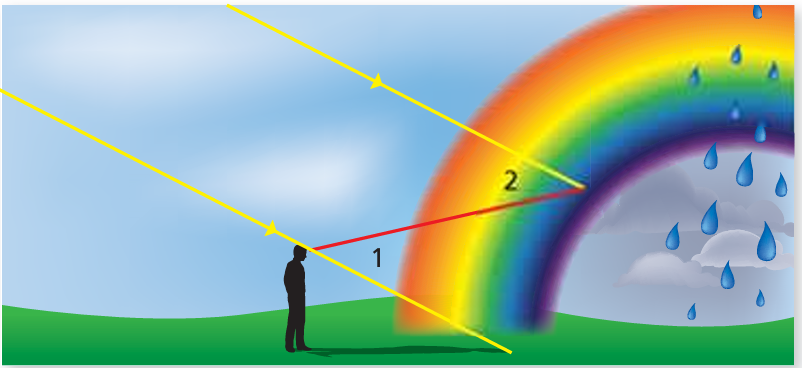
Solution :

Given that, ∠2 = 40

Since ∠1 and ∠2 are vertically opposite angles, then they will be equal.

∠1 = 40

Example 16 :

Find the value of x.

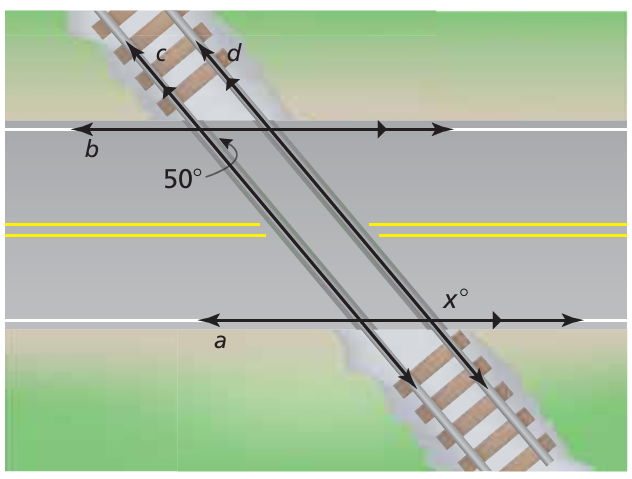
Solution :

50 + x = 180

x = 180 - 50

x = 130

So, the angle measure 130 degree.

Example 17 :

Find the value of x.

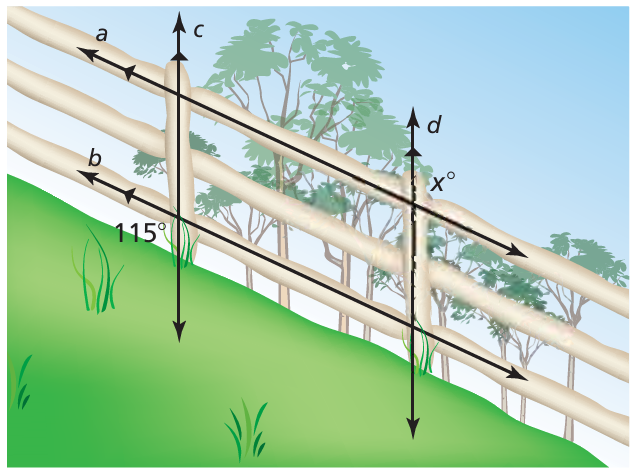
Solution :

x and 115 are alternate exterior angles. Then x = 115 degree.

Example 18 :

The figure shows the angles used to make a double bank shot in an air hockey game.

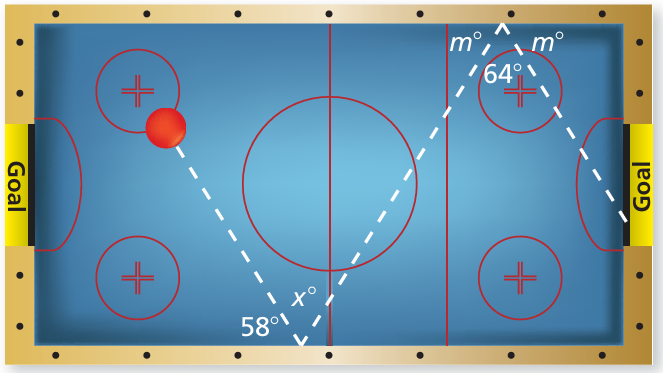
a. Find the value of x.

b. Can you still get the red puck in the goal if x is increased by a little? by a lot? Explain.

Solution  :

a)

m + 64 + m = 180

2m + 64 = 180

2m = 180 - 64

2m = 116

m = 116/2

m = 58

x = 64

b)  Yes, you can still get the red puck in the goal if x is increased by a little, but not if it's increased by a lot

Example 19 :

In Figure, ABCD is a trapezium such that AB||DC. Find ∠D and ∠C and verify that sum of the four angles is 360o.

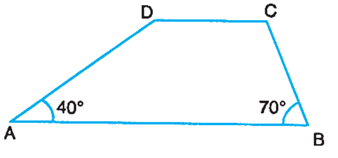
Solution :

Since the given figure ABCD is a trapezium, ∠A and ∠D are cointerior angles.