HOW TO FIND THE AREA OF A TRIANGLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
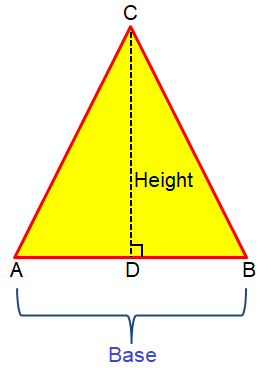
In the above figure, ABC is a triangle.
The formula to find the area of any triangle is
Area of a triangle = 1/2 × base × height
In figure, AB = base and CD = height
Area = 1/2 × AB × CD
Find the area of each triangle :
Problem 1 :
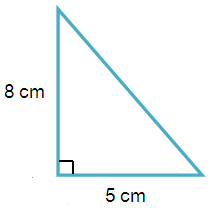
Solution :
By observing the figure,
Base (b) = 5 cm and Height (h) = 8 cm
Area of a triangle A = 1/2 (b × h)
= 1/2 (5 × 8)
Area = 20 cm2
Problem 2 :
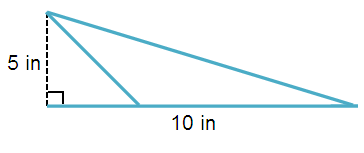
Solution :
By observing the figure,
Base (b) = 10 in and Height (h) = 5 in
Area of a triangle A = 1/2 (b × h)
= 1/2 (10 × 5)
= 25 in2.
Problem 3 :
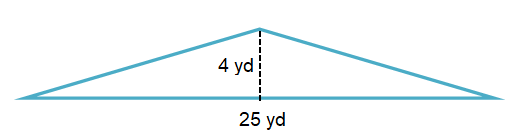
Solution :
By observing the figure,
Base (b) = 25 yd and Height (h) = 4 yd
Area of a triangle A = 1/2 (b × h)
= 1/2 (25 × 4)
= 50 yd2
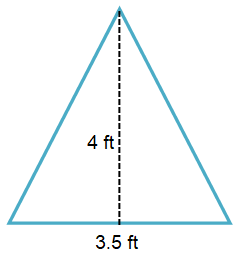
Problem 4 :
Solution :
By observing the figure,
Base (b) = 3.5 ft and Height (h) = 4 ft
Area of a triangle A = 1/2 (b × h)
= 1/2 (3.5 × 4)
= 7 ft2
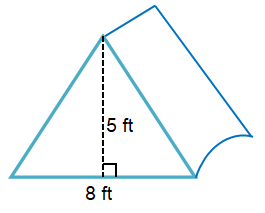
Problem 5 :
The front part of a tent is 8 feet long and 5 feet tall. what is the area of the front part of the tent ?
Solution :
Given,
The front part of a tent = 8 feet long
The front part of a tent = 5 feet tall
Area A = 1/2 (b × h)
Here base (b) = 8 feet and Height (h) = 5 feet
= 1/2 (8 × 5)
= 20 cm2
So, the area of the front part of the tent is 20 cm2.
Problem 6 :
Kathy is playing a board game. The game pieces are each in the shape of a triangle. Each triangle has a base of 1.5 inches and a height of 2 inches. What is the area of a game piece?
Solution :
Given,
Base of a game piece (b) = 1.5 inches
Height of a game piece (h) = 2 inches
To find the area of a game piece,
Area of a triangle A = 1/2 (b × h)
= 1/2 (1.5 × 2)
Area = 1.5 in2.
So, the area of a game piece = 1.5 in2.
Problem 7 :
A triangular – shaped window has a base of 3 feet and a height of 4 feet. What is the area of the window ?
Solution :
Given,
Base of the window (b) = 3 feet
Height of the window (h) = 4 feet
To find the area of the window,
Area of a triangle A = 1/2 (b × h)
= 1/2 (3 × 4)
Area = 6 ft2
So, the area of the window = 6 ft2.
Problem 8 :
Landon has a triangular piece of paper. The base of the paper is 6 1/2 inches. The height of the paper is 8 inches. What is the area of the piece of paper ?
Solution :
Given,
Base of the paper (b) = 6 1/2 inches
Height of the paper (h) = 8 inches.
To find the area of the piece of paper,
Area of a triangle A = 1/2 (b × h)
= 1/2 ((6/2) × 8)
= 1/2 (3 × 8)
= 1/2 (24)
= 12 in2
So, the area of the piece of paper = 12 in2.
Problem 9 :
A shelf has the shape of a triangle. The base of the shelf is 36 centimeters, and the height is 18 centimeters. Find the area of the shelf.
Solution :
Base = 36 cm, height = 18 cm
Area of triangle shelf = (1/2) x base x height
= (1/2) x 36 x 18
= 18 x 18
= 324 square cm.
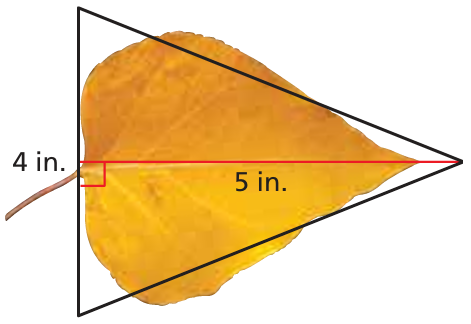
Problem 10 :
Estimate the area of the cottonwood leaf.
Solution :
Area of cotton wood = 1/2 x 4 x 5
= 2 x 5
= 10 square inches
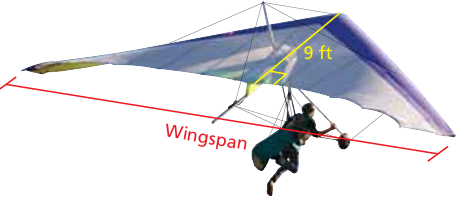
Problem 11 :
The wingspan of the triangular hang glider is 30 feet.
a. How much fabric is needed to make the sail?
Solution :
Base = 30 ft and height = 9 ft
Area of triangle = (1/2) x 30 x 9
= 15 x 9
= 135 square feet
Problem 12 :
The base and the height of Sail B are x times greater than the base and the height of Sail A. How many times greater is the area of Sail B? Write your answer as a power.
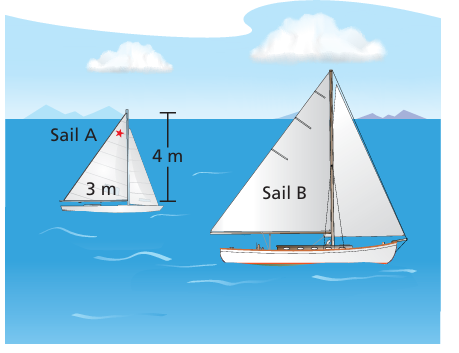
Solution :
Area of sail A = (1/2) x 3 x 4
= 6 square meter
Area of sail B = (1/2) ⋅ 3x ⋅ 4x
= 6x2 square meter
So, area of Sail B is x2 square meter greater than area of Sail A.
Problem 13 :
If the area of a square with side a is equal to the area of a triangle with base a then the altitude of the triangle is :
a) a/2 b) a c) 2a d) 4a
Solution :
Area of square with side length a = a2
Area of square = area of triangle
a2 = (1/2) x a x height
a2 = (a/2) x height
height = 2a2/a
= 2a
So, the altitude of the triangle is 2a, option c is correct.
Problem 14 :
If the area of triangle is 1176 cm2 and base corresponding altitude is 3 : 4, then the altitude of the triangle is :
a) 42 cm b) 52 cm c) 54 cm d) 56 cm
Solution :
Area of the triangle = 1176 cm2
Base = 3x and height = 4x
(1/2) ⋅ 3x ⋅ 4x = 1176
6x2 = 1176
x2 = 1176/6
x2 = 196
x = 14
Base = 3(14) ==> 42 cn
Height = 4(14) ==> 56 cm
So, the altitude is 56 cm, option d is correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling