EXPONENTS RULES WORKSHEET

Product Rule of Exponents 

Problem 1 :

a ⋅ a² ⋅ a³

Solution

Problem 2 :

(2a²b)(4ab²)

Solution

Problem 3 :

(6x²)(-3x⁵)

Solution

Problem 4 :

b³ ⋅ b⁴ ⋅ b⁷⋅ b

Solution

Problem 5 :

(3x³) (3x⁴) (-3x²)

Solution

Problem 6 :

(-5)^-10 ⋅ (-5)¹⁵

Solution

Problem 7 :

(4/5)^-6 ⋅ (4/5)^-9

Solution

Problem 8 :

(1.4)^-12 ⋅ (1.4)⁵

Solution

Problem 9 :

(-7/6)^-6 ⋅ (-7/6)³

Solution

Problem 10 :

(-13)⁰ ⋅ (-13)^-19

Solution

Problem 11 :

8^-14 ⋅ 8⁴

Solution

Problem 12 :

10^x ⋅ 10^-9 = 10¹¹

Solution

Problem 13 :

(-8/7)^-x⋅(-8/7)^-15=(-8/7)^-10

Solution

Problem 14 :

(-2.9)^-13⋅(-2.9)^x = (-2.9)^-5

Solution

Problem 15 :

The human body has about 100 billion cells. This number can be written in exponential form as

(a) 10^–11      (b) 10¹¹     (c) 10⁹    (d) 10^–9

Solution

Problem 16 :

(-2)³ ⋅ (-2)⁷ / (3 ⋅ 4⁶)

Solution

Problem 17 :

The value of (–2)^{2×3 –1} is

(a) 32     (b) 64    (c) – 32     (d) – 64

Solution

Problem 18 :

(2^-1 + 4^–1 + 6^–1 + 8^–1)^x = 1

Solution

Problem 19 :

Find the value of x^–3 if x = (100)^{1 - 4} ÷ (100)⁰

Solution

Problem 20 :

By what number should we multiply (–29)⁰ so that the product becomes (+29)⁰.

Solution

Problem 21 :

By what number should (–15)^–1 be divided so that quotient may be equal to (–15)^–1?

Solution

Problem 22 :

Find the multiplicative inverse of (–7)^–2 ÷ (90)^–1

Solution

Problem 23 :

If 5^3x–1 ÷ 25 = 125, find the value of x.

Solution

Problem 1 :

(x³)/x

Solution

Problem 2 :

(18c³)/(-3c²)

Solution

Problem 3 :

(9a³b⁵)/(-3ab²)

Solution

Problem 4 :

(-48c²d⁴)/(-8cd)

Solution

Problem 5 :

(22y⁶z⁸)/2yz^-7

Solution

Problem 6 :

(2x³)/(-8x⁴)

Solution

Problem 7 :

(xy⁷)/x³y⁴

Solution

Problem 8 :

6x⁵ ⋅ 3x⁵ ⋅ x⁰

Solution

Problem 9 :

(3st¹²)³

Solution

Problem 10 :

[(3m²n⁷)/m]⁵

Solution

Problem 11 :

(20x^-4/27y²) ÷ (8x^-3/15y^-5)

Solution

Simplify the expression. Write your answer as a power.

Problem 12 :

(7⁵ ⋅ 7³)/7²

Solution

Problem 13 :

(2.5)¹¹ / (2.5)^-x = (2.5)¹⁵

Solution

Problem 14 :

(-4/5)¹⁸ ÷ (-4/5)^-x = (-4/5)¹⁴

Solution

Problem 15 :

The table shows the volumes of the largest gaint sequoia trees. Which tree has the greatest volume ? How much greater is its volume than the other tree ?

Solution

Problem 16 :

A byte is a unit used to measure a computer’s memory. The table shows the numbers of bytes in several units of measure

a. How many kilobytes are in 1 terabyte?

b. How many megabytes are in 16 gigabytes?

c. Another unit used to measure a computer’s memory is a bit. There are 8 bits in a byte. How can you convert the number of bytes in each unit of measure given in the table to bits? Can you still use a base of 2? Explain.

Solution

Problem 17 :

Consider Cube A and Cube B.

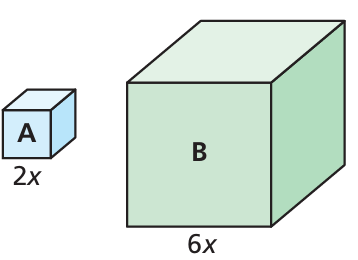
a. Which property of exponents should you use to simplify an expression for the volume of each cube?

b. How can you use the Power of a Quotient Property to find how many times greater the volume of Cube B is than the volume of Cube A?

Solution

Power Rule of Exponents

Simplify :

Problem 1 :

 (-2x⁴y⁴)²

Solution

Problem 2 :

(-a⁴b³)³

Solution

Problem 3 :

(-x³)²

Solution

Problem 4 :

(4a⁴b²)²

Solution

Problem 5 :

(yx²)³

Solution

Problem 6 :

(-4nm⁴)⁴

Solution

Problem 7 :

 (a⁴)²

Solution

Problem 8 :

 (-4y⁴)³

Solution

Problem 9 :

 (-3y³)³

Solution

Problem 10 :

 (-2x²)³

Solution

Problem 11 :

(-3xy³)⁴

Solution

Problem 12 :

(-2y²)²

Solution

Problem 13 :

(3y)³

Solution

Problem 14 :

(-2yx⁴)²

Solution

Problem 15 :

Evaluate the expression : -2² + (-3)²

Solution

Problem 16 :

Evaluate the expression : 

(4⁸ ⋅ m⁷⋅ n⁴)/(4⁵ ⋅ m²)

Solution

Problem 17 :

(9²) ^1/3

Solution

Problem 18 :

(12²) ^1/4

Solution

Problem 19 :

6/(6^1/4)

Solution

Problem 20 :

7/(7^1/3)

Solution

Problem 21 :

(8⁴/10⁴)^-1/4

Solution

Problem 22 :

(9³/6³)^-1/3

Solution

Problem 23 :

(3^-2/3⋅ 3^1/3)^-1

Solution

Problem 24 :

(5^1/2 ⋅ 5^-3/2)^-1/4

^Solution

Problem 25 :

(2^2/3 ⋅ 16^2/3) / 4^2/3

Solution

Problem 26 :

(49^3/8 ⋅ 49^7/8) / 7^5/4

^Solution

Problem 27 :

Write (2²)³ × 3⁶ in simplified exponential form.

Solution

Problem 28 :

Find the value of x if [(3/7)³]^-2 = (3/7)^2x 

Solution

Problem 29 :

Find the value of x if (-7/11)^-3 (-7/11)^-5x= [(-7/11)^-2]^-1

Solution

Problem 30 :

Find the value of x if (3/7)^-2x+1 ÷ (3/7)^-1 = [(3/7)^-1]^-7

Solution

Problem 31 :

Find the value of x if 2^{2x - 3} = (64)^x, find the value of x.

Solution