POWER RULE OF EXPONENTS

Power Rule of Exponents :

When an exponential expression is raised to a power, we have to multiply the exponent with the power.

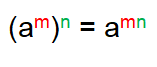
Example 1 :

(-2x⁴y⁴)²

Solution :

= (-2x⁴y⁴)²

First we distribute the power for all the terms which are inside the bracket that are multiplying.

= (-2)² (x⁴)² (y⁴)²

Evaluating (-2)², we get 4. Power raised by another power, so we have to multiply the powers.

= 4x⁸y⁸

Example 2 :

(-a⁴b³)³

Solution :

= (-a⁴b³)³

Distributing the power for all the terms which ar inside the bracket.

= (-a⁴)³ (b³)³

= -a¹²b⁹

Example 3 :

(-x³)²

Solution :

= (-x³)²

Since we have even number as power, by using the even power we change the negative exponent to positive.

= (x³)²

Raising power by another power, we will multiply the powers.

= x⁶

Example 4 :

(4a⁴b²)²

Solution :

= (4a⁴b²)²

Distributing the power for all the terms which are inside the bracket.

= 4²(a⁴)²(b²)²

Using power rule, we get

= 16a⁸b⁴

Example 5 :

(yx²)³

Solution :

= (yx²)³

= y³(x²)³

= y³x⁶

Example 6 :

(-4nm⁴)⁴

Solution :

= (-4nm⁴)⁴

= (-4)⁴(n)⁴(m⁴)⁴

= 256n⁴m¹⁶

Example 7 :

(a⁴)²

Solution :

= (a⁴)²

= a⁸

Example 8 :

(-4y⁴)³

Solution :

= (-4y⁴)³

= (-4)³(y⁴)³

= -64y¹²

Example 9 :

(-3y³)³

Solution :

= (-3y³)³

= (-3)³ (y³)³

= -27y⁹

Example 10 :

(-2x²)³

Solution :

= (-2x²)³

= (-2)³(x²)³

= -8x⁶

Example 11 :

(-3xy³)⁴

Solution :

= (-3xy³)⁴

= (-3)⁴ x⁴ (y³)⁴

= 81x⁴y¹²

Example 12 :

(-2y²)²

Solution :

= (-2y²)²

By distributing the powers for all the terms inside the bracket, we get

= (-2)²(y²)²

= 4y⁴

Example 13 :

(3y)³

Solution :

= (3y)³

By distributing the powers for all the terms inside the bracket, we get

= (3)³y³

= 27y³

Example 14 :

(-2yx⁴)²

Solution :

= (-2yx⁴)²

By distributing the powers for all the terms inside the bracket, we get

= (-2)²y²(x⁴)²

= 4y²x⁸

Example 15 :

Evaluate the expression : -2² + (-3)²

Solution :

= -2² + (-3)²

= -4 + 9

= 5

Example 16 :

Evaluate the expression : 

(4⁸ ⋅ m⁷⋅ n⁴)/(4⁵ ⋅ m²)

Solution :

= (4⁸ ⋅ m⁷⋅ n⁴)/(4⁵ ⋅ m²)

= (4⁸ / 4⁵) ⋅ (m⁷/ m²) n⁴

= 4^8-5  m^7-2 n⁴

= 4³  m⁵ n⁴

Example 17 :

(9²) ^1/3

Solution :

= (9²) ^1/3

Writing 9 in expanded form, we get 

9 = 3²

= ((3²)²) ^1/3

Sicne we ahve power raised by other powers, we have to multiply the powers. Then,

= 3^{2 x 2 x (1/3)}

= 3^4/3

Example 18 :

(12²) ^1/4

Solution :

= (12²)^1/4

= 12^2x(1/4)

= 12^(1/2)

Expressing the power as 1/2 and writing down as sqaure root, both are the same.

= √12

= √(2 x 2 x 3)

= 2√3

Example 19 :

6/(6^1/4)

Solution :

= 6/(6^1/4)

= 6¹/(6^1/4)

= 6^{1 - 1/4}

= 6^3/4

Example 20 :

7/(7^1/3)

Solution :

= 7/(7^1/3)

= 7¹/(7^1/3)

= 7^{1 - 1/3}

= 7^2/3

Example 21 :

(8⁴/10⁴)^-1/4

Solution :

= (8⁴/10⁴)^-1/4

Since we have same power for both numerator and denominator, we can write the same power.

= ((8/10)⁴)^-1/4

= (8/10)^4x(-1/4)

= (8/10)^-1

= 1/(8/10)¹

= 10/8

Simplifying it, we get

= 5/4

Example 22 :

(9³/6³)^-1/3

Solution :

= (9³/6³)^-1/3

Since we have same power for both numerator and denominator, we can write the same power.

= ((9/6)³)^-1/3

= (3/2)^3x(-1/3)

= (3/2)^-1

= 1/(3/2)¹

= 2/3

Example 23 :

(3^-2/3⋅ 3^1/3)^-1

Solution :

= (3^-2/3⋅ 3^1/3)^-1

Since the terms are multiplied, we put only one base and add the powers.

= (3^{-2/3 + 1/3})^-1

= (3^(-2+1)/3)^-1

= (3^-1/3)^-1

= 3^(-1/3)(-1)

= 3^(1/3)

Example 24 :

(5^1/2 ⋅ 5^-3/2)^-1/4

Solution :

= (5^1/2 ⋅ 5^-3/2)^-1/4

= (5^{1/2 - 3/2})^-1/4

= (5^(1-3)/2)^-1/4

= (5^-2/2)^-1/4

= (5^-1)^-1/4

= 5^{-1 x (-1/4)}

= 5^(1/4)

Example 25 :

(2^2/3 ⋅ 16^2/3) / 4^2/3

Solution :

= (2^2/3 ⋅ 16^2/3) / 4^2/3

16 can written in exponential form as 2⁴

= (2^2/3 ⋅ (2⁴)^2/3) / 4^2/3

= (2^2/3 ⋅ 2^8/3) / (2²)^2/3

= (2^2/3 ⋅ 2^8/3) / 2^4/3

= 2^{2/3 + 8/3 - 4/3}

= 2^(2+8-4)/3

= 2^6/3

= 2²

= 4

Example 26 :

(49^3/8 ⋅ 49^7/8) / 7^5/4

Solution :

= (49^3/8 ⋅ 49^7/8) / 7^5/4

= (49^3/8+7/8) / 7^5/4

= (49^(3+7)/8) / 7^5/4

= (49^10/8) / 7^5/4

= (49^5/4) / 7^5/4

= ((7²)^5/4) / 7^5/4

= 7^10/4 / 7^5/4

= 7^{10/4 - 5/4}

= 7^{(10 - 5)/4}

= 7^5/4

Example 27 :

Write (2²)³ × 3⁶ in simplified exponential form.

Solution :

= (2²)³ × 3⁶

= 2⁶ × 3⁶

Since we have same power and the bases are multiplied, we use only one power.

= (2 × 3)⁶

= 6⁶

Example 28 :

Find the value of x if [(3/7)³]^-2 = (3/7)^2x 

Solution :

[(3/7)³]^-2 = (3/7)^2x 

(3/7)^-6 = (3/7)^2x 

-6 = 2x

x = -6/2

x = -3

Example 29 :

Find the value of x if (-7/11)^-3 (-7/11)^-5x= [(-7/11)^-2]^-1

Solution :

(-7/11)^-3 (-7/11)^-5x = [(-7/11)^-2]^-1

(-7/11)^-3-5x = (-7/11)²

3 - 5x = 2

-5x = 2 - 3

-5x = -1

x = 1/5

Example 30 :

Find the value of x if (3/7)^-2x+1 ÷ (3/7)^-1 = [(3/7)^-1]^-7

Solution :

(3/7)^-2x+1 ÷ (3/7)^-1 = [(3/7)^-1]^-7

(3/7)^-2x+1+1 = (3/7)⁷

-2x + 1 = 7

-2x = 7 - 1

-2x = 6

x = -3

Example 30 :

Find the value of x if 2^{2x - 3} = (64)^x, find the value of x.

Solution :

2^{2x - 3} = (64)^x

2^{2x - 3} = (2⁶)^x

2^{2x - 3} = 2^6x

2x - 3 = 6x

2x - 6x = 3

-4x = 3

x = -3/4