QUOTIENT RULE OF EXPONENTS

Example 1 :

Solution :

Example 2 :

Solution :

Example 3 :

Solution :

Example 4 :

Solution :

Example 5 :

Solution :

Example 6 :

Solution :

Example 7 :

Solution :

Example 8 :

6x⁵ ⋅ 3x⁵ ⋅ x⁰

Solution :

Multiply the coefficients,

= 6x⁵ ⋅ 3x⁵ ⋅ x⁰

= (6 × 3)(x⁵ ⋅ x⁵ ⋅ x⁰)

By a^m ⋅ aⁿ = a^m+n,

= 18(x⁵⁺⁵ ⋅ x⁰)

= 18(x¹⁰⋅ x⁰)

= 18x¹⁰

Example 9 :

(3st¹²)³

Solution :

= (3st¹²)³

= 3³s³(t¹²)³

= 27s³(t¹²)³

By (a^m)ⁿ = a^mn,

= 27s³t^(12×3)

=  27s³t³⁶

Example 10 :

Solution :

Example 11 :

Solution :

Simplify the expression. Write your answer as a power.

Example 12 :

(7⁵ ⋅ 7³)/7²

Solution :

= (7⁵ ⋅ 7³)/7²

= 7^{(5 + 3)} / 7²

= 7⁸/7²

= 7^{8 - 2}

= 7⁶

Example 12 :

(2.5)¹¹ / (2.5)^-x = (2.5)¹⁵

Solution :

(2.5)¹¹ / (2.5)^-x = (2.5)¹⁵

Using the quotient rule of exponents,

(2.5)^11+x = (2.5)¹⁵

Since the bases are same, we can equate the powers.

11 + x = 15

x = 15 - 11

x = 4

11 + x 

Example 13 :

(-4/5)¹⁸ ÷ (-4/5)^-x = (-4/5)¹⁴

Solution :

(-4/5)¹⁸ ÷ (-4/5)^-x = (-4/5)¹⁴

(-4/5)^{18 + x} = (-4/5)¹⁴

18 + x = 14

x = 14 - 18

x = -4

Example 14 :

The table shows the volumes of the largest gaint sequoia trees. Which tree has the greatest volume ? How much greater is its volume than the other tree ?

Solution :

General sherman is heavier than Washington tree.

= (5.25 x 10⁴) / (4.785 x 10⁴)

= (5.25 /4.785)

= 1.09

General sherman is 1.09 times heavier than Washington.

Example 15 :

A byte is a unit used to measure a computer’s memory. The table shows the numbers of bytes in several units of measure

a. How many kilobytes are in 1 terabyte?

b. How many megabytes are in 16 gigabytes?

c. Another unit used to measure a computer’s memory is a bit. There are 8 bits in a byte. How can you convert the number of bytes in each unit of measure given in the table to bits? Can you still use a base of 2? Explain.

Solution :

a. Number of kilobytes in 1 ter byte = 2⁴⁰ / 2¹⁰

= 2^{40 - 10}

= 2³⁰

b. Number of bytes in 1 gigabyte = 2³⁰

Number of bytes in 16 gigabyte = 16(2³⁰)

Number of megabytes in 16 gigabyte = 16(2³⁰) / (2²⁰)

= 16(2¹⁰)  

= 16384

c. 1 byte = 8 bits

To convert the number of bytes in each unit of measure given in the table to bits using a base of 2, we know that there are 8 bits in a byte. Therefore, to convert the number of bytes to bits, we can multiply the number of bytes by 8.

Example 16 :

Consider Cube A and Cube B.

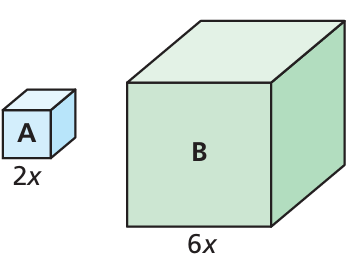
a. Which property of exponents should you use to simplify an expression for the volume of each cube?

b. How can you use the Power of a Quotient Property to find how many times greater the volume of Cube B is than the volume of Cube A?

Solution :

a)

Using the product rule, we evaluate the volumes of each cubes.

b)  Volume of cube B is greater than volume of cube A.

Number of times = 216x³ / 8x³

= 27x³

Using quotient rule, we find the number of times.