CONVERTING BETWEEN STANDARD VERTEX AND FACTORED FORM

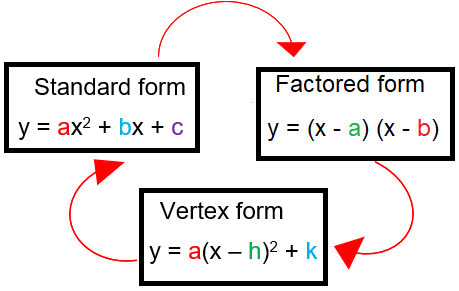
Given one of the forms of a quadratic function, convert to the other two forms.

Problem 1 :

y = x² − 6x − 7

(i) Vertex form

(ii)  Factored form

Solution :

(i) Converting into vertex form :

y = x² − 6x − 7

Coefficient of x² is 1. So, don't have to factories anything.

Write the coefficient of x as multiple of 2. 

y = x² − 2⋅x⋅3 + 3² - 3² - 7

y = (x - 3)² - 3² - 7

y = (x - 3)² - 9 - 7

y = (x - 3)² - 16

y = (x - h)² + k

Vertex (h, k) is (3, -16).

(i) Converting into factored form :

y = x² − 6x − 7

Decomposing -7, we get 1 (-7).

1(-7) = -7, 1 + (-7) = -6

y = x² + 1x - 7x − 7

y = x(x + 1) - 7(x + 1)

y = (x + 1) (x - 7)

So, -1 and 7 are x-intercepts.

Problem 2 :

y = 3(x − 1)² − 3

(i) Standard form 

(ii) Factored form

Solution :

(i) Converting into standard form :

y = 3(x − 1)² − 3

Here (x-1)² looks like (a - b)².

(a - b)² = a² - 2ab + b²

(x − 1)² = x² - 2x(1) + 1²

(x − 1)² = x² - 2x - 3

y = 3(x² - 2x + 1) - 3

y = 3x² - 6x + 3 - 3

y = 3x² - 6x

(ii) Converting into factored form :

y = 3x² - 6x

Factor 3x, we get

= 3x (x - 2)

So, 0 and 2 are x-intercepts.

Problem 3 :

y = 2(x − 3)(x + 5)

(i) Vertex form:

(ii) Standard form:

Solution :

(i) Converting into vertex form :

y = 2(x − 3)(x + 5)

y = 2(x² + 5x - 3x - 15)

y = 2(x² + 2x - 15)

y = 2(x² + 2⋅x⋅1 + 1² - 1² - 15)

y = 2[(x + 1)² - 1² - 15]

y = 2[(x + 1)² - 16]

y = 2(x + 1)² - 32

So, vertex is (-1, -32).

(ii) Converting into standard form :

y = 2(x − 3)(x + 5)

y = 2(x − 3)(x + 5)

y = 2(x² + 5x - 3x - 15)

y = 2(x² + 2x - 15)

Distributing 2, we get

y = 2x² + 4x - 30

Problem 4 :

y = 2x² + 8x + 10

(i) Vertex form:

(ii) Factored form

Solution :

(i) Converting into vertex form :

y = 2x² + 8x - 10

y = 2(x² + 4x - 5)

y = 2(x² + 2⋅x⋅2 + 2² - 2² - 5)

y = 2[(x+2)² - 4 - 5)]

y = 2[(x+2)² - 9]

y = 2(x+2)² - 18

So, the vertex is (-2, -18).

(ii) Converting into factored form :

y = 2x² + 8x - 10

y = 2(x² + 4x - 5)

y = 2(x - 5² + 4x - 5)

Problem 5 :

𝑦 = 2(𝑥 + 1)² − 8

(i)  Standard form

(ii)  Factored form

Solution :

(i) Converting into standard form :

𝑦 = 2(𝑥 + 1)² − 8

Using the algebraic identity (a + b)², we can find the expansion of (x + 1)²

(x + 1)² = x² + 2⋅x⋅1 + 1²

(x + 1)² = x² + 2x + 1

y = 2(x² + 2x + 1) − 8

y = 2x² + 4x + 2 − 8

y = 2x² + 4x − 6

(ii) Converting into factored form :

y = 2x² + 4x − 6

Factoring 2, we get

y = 2(x² + 2x − 3)

y = 2(x - 1) (x + 3)

Problem 6 :

y = −4(x + 1)(2x − 5)

(i) Vertex form:

(ii)  Standard form:

Solution :

(i) Converting into vertex form :

y = −4(x + 1)(2x − 5)

y = −4(2x² - 5x + 2x - 5)

y = −4(2x² - 3x - 5)

y = −4(2x² - 3x - 5)

So, the vertex is (3/4, 49/2).

(ii) Converting into standard form :

y = −4(x + 1)(2x − 5)

y = −4(2x² - 5x + 2x - 5)

y = −4(2x² - 3x - 5)

y = −4(2x² - 3x - 5)

y = −8x² + 12x + 20

Problem 7 :

Flying fish use  Let the graph of g be a their pectoral fins like airplane wings to glide through the air.

a. Write an equation of the form y = a(x − h)² + k with vertex (33, 5) that models the flight path, assuming the fish leaves the water at (0, 0).

b. What are the domain and range of the function? What do they represent in this situation?

c. Does the value of a change when the flight path has vertex (30, 4)? Justify your answer.

Solution :

a) y = a(x − h)² + k

Here the vertex is (33, 5)

y = a(x − 33)² + 5

Since it passes through (0, 0), we get

0 = a(0 − 33)² + 5

0 = a(33)² + 5

-5 = a(1089)

a = -5/1089

y = (-5/1089) (x − 33)² + 5

that models the flight path, assuming the fish leaves the water at (0, 0).

b. Domain is (0, ∞)

The parabola opens down. Range is (5, -∞)

c. Applying the new vertex (30, 4) and find the value of a by applying (0, 0) we get

y =  a(x − 30)² + 4

0 =  a(0 − 30)² + 4

0 = a(900) + 4

900a = -4

a = -4/900

a = -1/225

y =  (-1/225)(x − 30)² + 4

The path will change.