SMO JUNIOR SECTION 2012

Problem 1 :

Let α and β be the roots of the quadratic equation

x² + 2bx + b = 1

The smallest possible value of (α - β)²

(A)  0     (B) 1      (C)  2    (D)  3     (E)  4

Solution

Problem 2 :

It is known that n²⁰¹² + n²⁰¹⁰ is divisible by 10 for some positive integer n. Which of the following numbers is not a possible value for n?

(A) 2    (B) 13     (C) 35     (D) 47    (E) 59

Solution

Problem 3 :

Using the vertices of a cube as vertices , how many triangular pyramid can you form?

(A) 54   (B) 58     (C) 60    (D) 64     (E) 70

Solution

Problem 4 :

AB is a chord of a circle with center 0. CD is the diameter perpendicular to the chord AB, with AB closer to C than to D. Given that  ∠.AOB = 90° , then the quotient

area of △ABC/area of △AOD = ?

(A) √2 - 1   (B) 2 - √2      (C) √2/2    (D) (1+√2)/2    (E) 1/2

Solution

Problem 5 :

The diagram below shows that ABCD is a parallelogram and both AE and BE are straight lines. Let F and G be the intersections of BE with CD and AC respectively. Given that BG = EF, find the quotient DE/ AE.

Solution

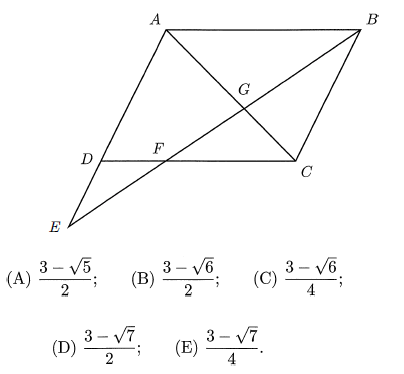
Problem 6 :

Four circles each of radius x and a square are arranged within a circle of radius 8 as shown in the following figure .

Solution

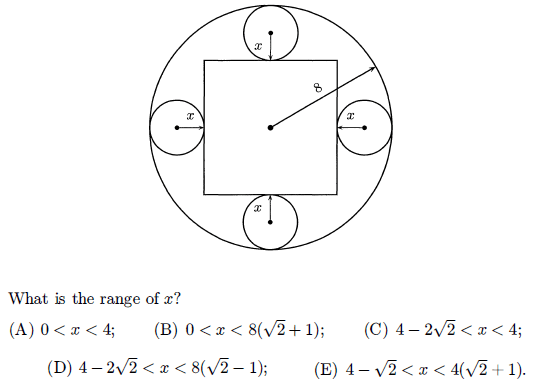
Problem 7 :

Adam has a triangular field ABC with AB = 5, BC = 8 and CA = 11. He intends to separate the field into two parts by  building a straight fence from A to a point D on side BC such that AD bisects ∠.BAC. Find the area of the part of the field ABD.

Solution

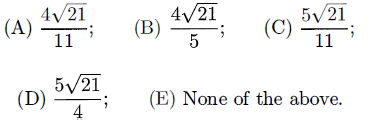
Problem 8 :

For any real number x, let ⌊x⌋ be the largest integer less than or equal to x and x = x - ⌊x⌋. Let a and b be real numbers with b ≠ 0 such that 

a = b⌊a/b⌋ - b{a/b}

which of the following is incorrect ?

(A) If b is an integer then a is an integer;

(B) If a is a non-zero integer then b is an integer;

(C) If b is a rational number then a is a rational number;

(D) If a is a non-zero rational number then b is a rational number;

(E) If b is an even number then a is an even number.

Solution

Problem 9 :

Given that

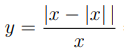
is an integer . Which of the following is incorrect?

(A) x can admit the value of any non-zero integer;

(B) x can be any positive number;

(C) x can be any negative number;

(D) y can take the value 2;

(E) y can take the value -2.

Solution

Problem 10 :

Suppose that A, B, C are three teachers working in three different schools X , Y, Z and specializing in three different subjects: Mathematics , Latin and Music . It is known that

(i) A does not teach Mathematics and B does not work in school Z;

(ii) The teacher in school Z teaches Music;

(iii) The teacher in school X does not teach Latin;

(iv) B does not teach Mathematics.

Which of the following statement is correct?

(A) B works in school X and C works in school Y;

(B) A teaches Latin and works in school Z;

(C) B teaches Latin and works in school Y;

(D) A teaches Music and C teaches Latin;

(E) None of the above.

Solution

Problem 11 :

Let a and b be real numbers such that a > b, 2^a + 2^b = 75 and 2^-a + 2^-b = 12^-1. Find the value of 2^a-b

Solution

Problem 12 :

Find the sum of all positive integers x such that 

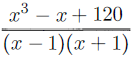
is an integer.

Solution

Problem 13 :

Consider the equation

√(3x²-8x+1) + √(9x²-24x-8) = 3

It is known that the largest root of the equation is - k times the smallest root . Find k.

Solution

Problem 14 :

Find the four digit number

Solution

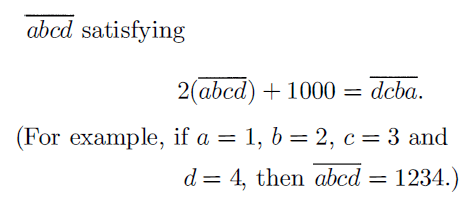
Problem 15 :

Suppose x and y are real number satisfying 

x² + y² - 22x - 20y + 221 = 0. Find xy.

Solution

Problem 16 :

Let m and n be positive integers satisfying 

mn² + 876 = 4mn + 217 n

Find the sum of all possible values of m.

Solution

Problem 17 :

For any real number x, let ⌊x⌋ denote the largest integer less than or equal to x. Find the value of ⌊x⌋ of the smallest x satisfying ⌊x²⌋ - ⌊x⌋² = 100.

Solution

Problem 18 :

Suppose x₁, x₂, .............x₄₉ are real numbers such that 

 x₁²+ 2x₂², .............49x₄₉² = 1

Find the maximum value of x₁+ 2x₂, .............49x₄₉

Solution

Problem 19 :

Find the minimum value of

√x² + (20 -y)² + √y² + (21 - z)² + √z² + (20 -w)² + √w² + (21 - x)²

Solution

Problem 20 :

Let A be a 4 digit number. When both the first digit(left most) and the third digit are increased by n, and the second digit and fourth digit are decreased by n, the new number is n times A. Find the value of A.

Problem 21 :

Find the remainder when 1021^I022 is divided by 1023.

Solution

Problem 31 :

How many triples of non-negative integers (x, y, z) satisfying the equation

xyz + xy + yz + zx + x + y + z = 2012?

Solution

Problem 35 :

There are k people and n chairs in a row, where 2≤ k < n. There is a couple among k people. The number of ways in which all k people can be seated such that the couple is seated together is equal to the number of ways in which the (k - 2) people without the couple present, can be seated. Find the smallest value of n.

Solution