SMO JUNIOR SECTION 2012 SOLUTIONS PART 3

Problem 7 :

Adam has a triangular field ABC with AB = 5, BC = 8 and CA = 11. He intends to separate the field into two parts by  building a straight fence from A to a point D on side BC such that AD bisects ∠.BAC. Find the area of the part of the field ABD.

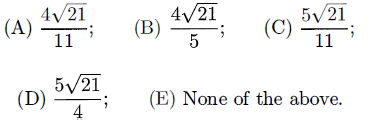
Solution :

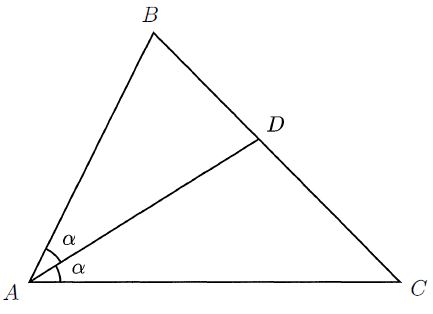
Here AB = 5, BC = 8 and CA = 11

Area of triangle ABC :

Area of triangle ABD = (1/2) x AD x BD

sin α = BD/AB

BD = AB sin α

Area of triangle ADC = (1/2) x AD x DC

sin α = DC/AC

DC = AC sin α

Ratio between the triangles ABD and ADC :

Applying the values of BD and DC respectively in the area, we get

Area of triangle ABD/Area of triangle ADC

= [(1/2) x AD x AB sin α] / [(1/2) x AD x AC sin α]

= AB/AC

= 5/11

So, option D is correct.

Problem 8 :

For any real number x, let ⌊x⌋ be the largest integer less than or equal to x and x = x - ⌊x⌋. Let a and b be real numbers with b ≠ 0 such that 

a = b⌊a/b⌋ - b{a/b}

which of the following is incorrect ?

(A) If b is an integer then a is an integer;

(B) If a is a non-zero integer then b is an integer;

(C) If b is a rational number then a is a rational number;

(D) If a is a non-zero rational number then b is a rational number;

(E) If b is an even number then a is an even number.

Solution :

The greatest integer function is a function that results in the integer nearer to the given real number.  The greatest integer function rounds off the given number to the nearest integer.

Given :

a = b⌊a/b⌋ - b{a/b}

a = b⌊a/b⌋ - b{a/b}

(A) If b is an integer, then b⌊a/b⌋ = integer and b{a/b} = integer, then a is also integer.

(B)  Let a be the integer and b be decimal, then (a/b) will be decimal, but ⌊a/b⌋ should be integer.

In b{a/b}, Obviously, b is not necessary an integer even if a is an integer.

So, option B is incorrect.

Problem 9 :

Given that

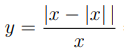
is an integer . Which of the following is incorrect?

(A) x can admit the value of any non-zero integer;

(B) x can be any positive number;

(C) x can be any negative number;

(D) y can take the value 2;

(E) y can take the value -2.

Solution :

If x > 0, for example x = 5

=  |5 - |5|| / 5

=  0/5

= 0

If x < 0, for example x = -5

=  |-5 - |-5|| / 5

=  |-5 - 5| / (-5)

= |-10| / (-5)

= 10 / (-5)

= -2

Option D is incorrect, even we give the negative value, the numerator will become a positive and the denominator only will have negative sign. So, the final answer may be negative. 

Why the value of x wouldn't  be 0 :

Because the question says, y is a integer. Yes 0 is also an integer.

Problem 10 :

Suppose that A, B, C are three teachers working in three different schools X , Y, Z and specializing in three different subjects: Mathematics , Latin and Music . It is known that

(i) A does not teach Mathematics and B does not work in school Z;

(ii) The teacher in school Z teaches Music;

(iii) The teacher in school X does not teach Latin;

(iv) B does not teach Mathematics.

Which of the following statement is correct?

(A) B works in school X and C works in school Y;

(B) A teaches Latin and works in school Z;

(C) B teaches Latin and works in school Y;

(D) A teaches Music and C teaches Latin;

(E) None of the above.

Solution :

B does not teach math and does not work in Z. He may work in X or Y and may teach the subjects Latin or Music.

The teacher is school X does not teach Latin. So, teacher in the that school may teach math or latin.

Considering option A :

B works in X or Y and C also works in X or Y. anything is possible. But we cannot say surely.

Considering option B :

Teacher A should not work in school X. he may work in Y or Z.

Considering option C:

If B teaches Latin, then he should work in Y only, because he will not work in X.

The assignment is as follows:

A: in Z, teaches Music; B: in Y , teaches Latin; C: in X , teaches Mathematics

So, option C is correct.