SMO JUNIOR SECTION 2012 SOLUTIONS PART 6

Problem 18 :

Suppose x₁, x₂, .............x₄₉ are real numbers such that 

 x₁²+ 2x₂², .............49x₄₉² = 1

Find the maximum value of x₁+ 2x₂, .............49x₄₉

Solution :

x₁²+ 2x₂², .............49x₄₉² = 1

x₁₊ (√2√2x₂)^2+..........(√49√49) x₄₉² = 1

1⋅1 x₁₊ (√2√2x₂)^2+..........(√49√49) x₄₉²  = 1 

= (1 + 2 + 3 +...........+49) (x₁²+ 2x₂², .............49x₄₉²)

Sum of natural numbers = n (n+1)/2

= [49(50)/2] ⋅ 1

= 49 ⋅ 25

= 1225

Problem 19 :

Find the minimum value of

√x² + (20 -y)² + √y² + (21 - z)² + √z² + (20 -w)² + √w² + (21 - x)²

Solution :

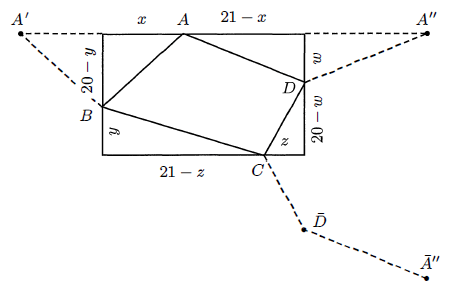
AB = A'B, CD = CD', AD = A''D',BC = BC 

AB + BC + CD +DA

= A'B + BC + CD + DA"

≤A' A" =  √ 42² + 40² = 58

So, the minimum value is 58.

Problem 20 :

Let A be a 4 digit number. When both the first digit(left most) and the third digit are increased by n, and the second digit and fourth digit are decreased by n, the new number is n times A. Find the value of A.

Solution :

Let A = abcd, then

1000a + 100b + 10c + d

1^st and 3^rd digit increase by n and 2^nd and 4^th digit are decreased by n.

1000(a + n) + 100(b - n) + 10(c + n) + d - n = nA

1000a + 1000n + 100b - 100n + 10c + 10n + d = nA

1000a + 100b + 10c + d + (1000-100+10-1)n = nA

A + 909n = nA

909n = nA - A

909n = A(n-1)

If n = 2

909 x 2 = A(2-1)

A = 1818

Problem 21 :

Find the remainder when 1021^I022 is divided by 1023.

Solution :

1021 is nearer to 1023

1021- 1023 = -2

= (-2)^I022 

= (2)^I022 

= (2)^I022 

= (2)^{I020 + 2}

= ((2)^I0)¹⁰² x 2² 

210  = 1024, dividing 1024 by 1023, we get 1 as remainder.

= 1¹⁰² x 4

= 4

So, the required remainder is 4.

Problem 31 :

How many triples of non-negative integers (x, y, z) satisfying the equation

xyz + xy + yz + zx + x + y + z = 2012?

Solution :

xyz + xy + yz + zx + x + y + z = 2012

Adding 1 both on both sides.

1 + x + y + z + xy + yz + zx + xyz = 2012 + 1

(1 + x) + (y + xy) + (z + zx) + (yz + xyz) = 2013

(1 + x) + y(1 + x) + z(1 + x ) + yz(1 + x) = 2013

Factoring (1+x), we get

(1 + x) (1 + y + z + yz) = 2013

(1 + x) [(1 + y) + z(1 + y))] = 2013

(1 + x)(1+y)(1+z)  = 2013

(1 + x)(1+y)(1+z)  = 3 x 11 x 61

If all x, y, z are positive, there are 3! = 6 solutions.

If exactly one of x, y, z is 0, there are 3 x 6 = 18 solutions.

If exactly two of x, y, z are 0, there are 3 solutions.

6 + 18 + 3 = 27

Problem 35 :

There are k people and n chairs in a row, where 2 ≤ k < n. There is a couple among k people. The number of ways in which all k people can be seated such that the couple is seated together is equal to the number of ways in which the (k - 2) people without the couple present, can be seated. Find the smallest value of n. 

Solution :

k people is seated in n chairs and the couple to be seated together. So,

(n - 1)! ways and

2! (The couple themselves can change the position)

In n chairs 2 chairs should be ignored and in k people 2 people should be ignored.

(n - 1)! 2! ^{(n - 2)}C_{(k - 2)} -------(1)

ⁿC_(k-2)-------(2)

Here √8k - 7 > 0

when k = 11

n = [4(11) -5±√8(11) - 7]/4

n = [44 -5±√81]/4

n = (39±9)/4

n = 48/4

n = 12