SMO JUNIOR SECTION 2012 SOLUTIONS PART 2

Problem 3 :

Using the vertices of a cube as vertices , how many triangular pyramid can you form?

(A) 54   (B) 58     (C) 60    (D) 64     (E) 70

Solution :

Problem 4 :

AB is a chord of a circle with center 0. CD is the diameter perpendicular to the chord AB, with AB closer to C than to D. Given that  ∠.AOB = 90° , then the quotient

area of △ABC/area of △AOD = ?

(A) √2 - 1   (B) 2 - √2      (C) √2/2    (D) (1+√2)/2    (E) 1/2

Solution :

Let radius of the circle be 1.

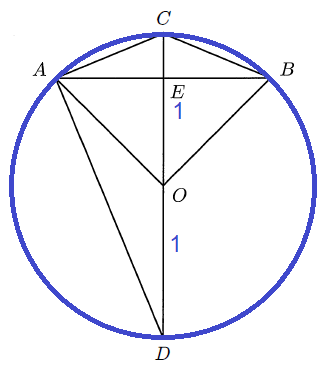
Area of triangle ABC = 2(Area of AEC)

= 2(1/2 x AC x AE) ==>  CE x AE  -----(1)

Area of triangle AOD = 1/2 x AE x OD  -----(2)

(1) / (2) 

= CE / (1/2) x 1

Area of triangle AOD = 2 CE

Here CE = OC - OE

Triangle AEO is 45-45-90 right triangle.

OA = radius = 1

OA² = AE² + EO²

1² = AE² + AE²

2(AE)² = 1

(AE)² = 1/2

AE = 1/√2 = OE

OE = √2/2

CE = 1 - (√2/2)

Area of triangle AOD = 2[1 - (√2/2)]

= 2[(2 - √2)/2]

= 2 - √2

So, option B is correct.

Problem 5 :

The diagram below shows that ABCD is a parallelogram and both AE and BE are straight lines. Let F and G be the intersections of BE with CD and AC respectively. Given that BG = EF, find the quotient DE/ AE.

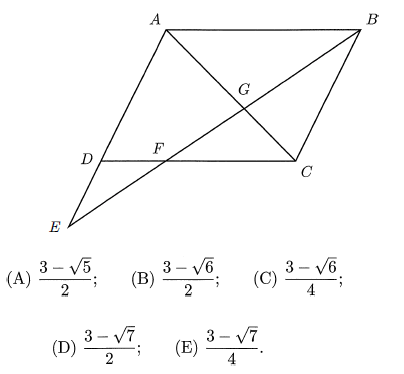
Problem 6 :

Four circles each of radius x and a square are arranged within a circle of radius 8 as shown in the following figure .

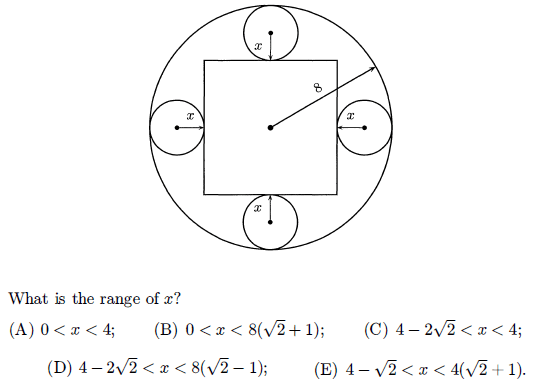
Solution :

To find the minimum value of x, enlarging square.

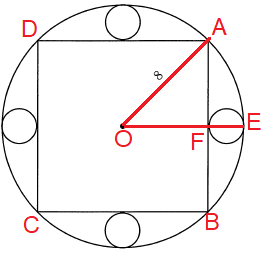
OA = OE = radii = 8

Triangle OAF is 45 - 45 - 90 degree special right triangle.

OA = hypotenuse

OA² = OF² + FA²

8² = OF² + OF²

2OF² = 64

OF² = 32

OF = √32

OF = 2√2

FE = OE - OF

FE (Diameter) = 8 - 2√2

Radius = (8 - 2√2)/2

= 4 - √2

By enlarging circle, we get

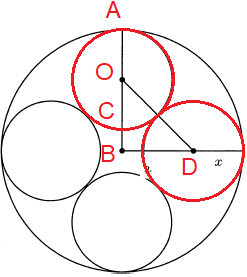
AB = 8, OA = x = OC, BC = unknown

AB = 8

AO + OC + CB = 8

x + x + CB = 8

CB = 8 - 2x,  BD =  8 - 2x + x ==> 8 - x

Triangle OBD,

OD² = OB² + BD²

(2x)² = (8 - x)² + (8 - x)²

4x2 = 2(8 - x)² 

2x² = (8 - x)² 

8-x = x√2

Now x√2 + x = 8

x(√2+1) = 8

So, option D is correct.