WRITING QUADRATIC EQUATION FROM GRAPHS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Determine the equation of quadratic function from graph. Give the function in general form.
Problem 1 :
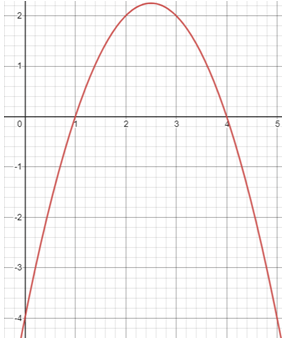
Problem 2 :
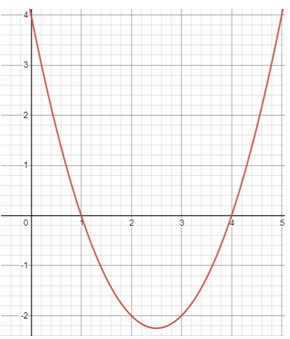
Problem 3 :
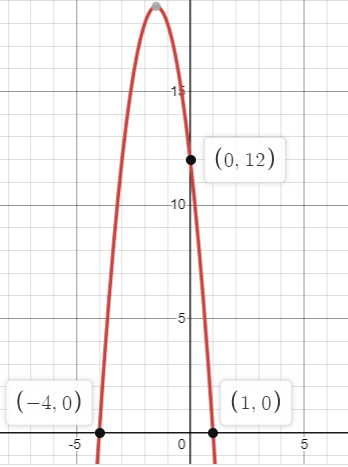
Problem 4 :
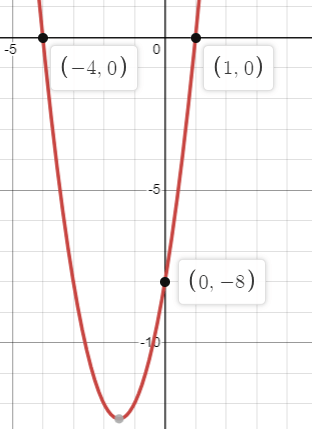
Problem 5 :
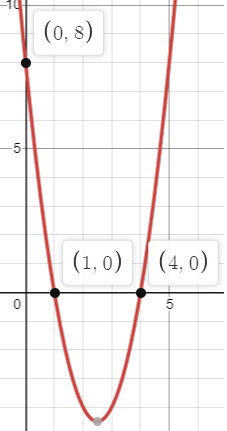
Problem 6 :
The area of a rectangle is modeled by the graph where y is the area (in square meters) and x is the width (in meters). Write an equation of the parabola. Find the dimensions and corresponding area of one possible rectangle. What dimensions result in the maximum area?
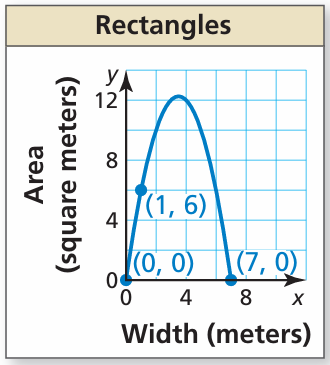
Problem 7 :
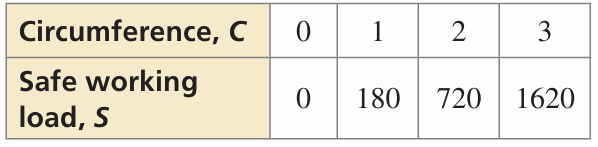
Every rope has a safe working load. A rope should not be used to lift a weight greater than its safe working load. The table shows the safe working loads S (in pounds) for ropes with circumference C (in inches). Write an equation for the safe working load for a rope. Find the safe working load for a rope that has a circumference of 10 inches.
Answer Key
1) y = -x2 + 5x - 4
2) y = x2 - 5x + 4
3) y = -3x2 - 9x + 12
4) y = 2x2 + 6x - 8
5) y = 2x2 - 10x + 8
6) f(x) = -x(x - 7)
7) y = 180x2
Determine the equation of quadratic function from graph. Give the function in vertex form.
Problem 1 :
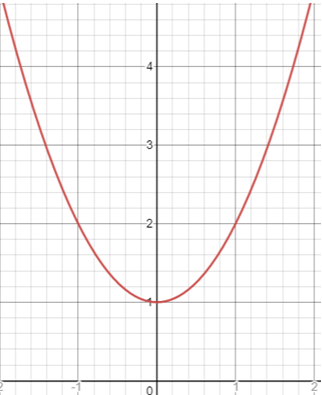
Problem 2 :
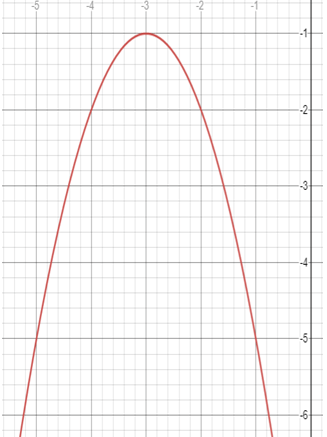
Problem 3 :
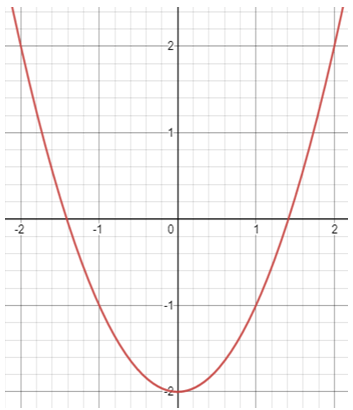
Problem 4 :
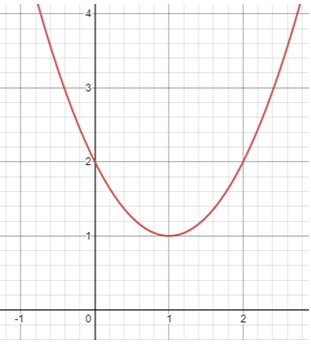
Problem 5 :
Which function represents the widest parabola? Explain your reasoning.
a) y = 2(x + 3)2 b) y = x2 − 5 c) y = 0.5(x − 1)2 + 1 d) y = −x2 + 6
Problem 6 :
The graph of which function has the same axis of symmetry as the graph of
y = x2 + 2x + 2?
a) y = 2x2 + 2x + 2 b) y = −3x2− 6x + 2
c) y = x2 − 2x + 2 d) y = −5 x2+ 10x + 2
Problem 7 :
The path of a diver is modeled by the function
f(x) = −9x2 + 9x + 1
where f(x) is the height of the diver (in meters) above the water and x is the horizontal distance (in meters) from the end of the diving board.
a. What is the height of the diving board?
b. What is the maximum height of the diver?
c. Describe where the diver is ascending and where the diver is descending.
Answer Key
1) y = x2 + 1
2) y = (x + 3)2 - 1
3) y = x2 - 2
4) y = 1(x - 1)2 + 1
5) option c is wider, y = 0.5(x − 1)2 + 1
6) y = −3x2− 6x + 2, option b
7) a) height of the board is 1 meter.
b) Reaches the maximum height at 0.5 seconds and the height is 3.25 m
c) When x > 0.5, it is increasing and x < 0.5 it is decreasing.
Problem 1 :
The roots of a quadratic equation are -2 and -6. The minimum point of the graph of its related function is at (-4, -2). Sketch the graph of the function.
Problem 2 :
The roots of a quadratic equation are -6 and 0. The minimum point of the graph of its related function is at (-3, 4). Sketch the graph of the function.
Problem 3 :
Which of the following x equations represent the parabola?
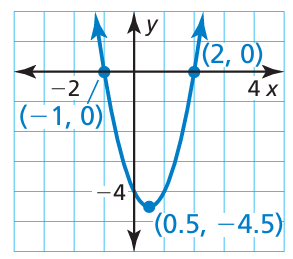
a) y = 2(x − 2)(x + 1) b) y = 2(x + 0.5)2 − 4.5 c) y = 2(x − 0.5)2 − 4.5
d) y = 2(x + 2)(x − 1)
Problem 4 :
x-intercepts of 12 and −6; passes through (14, 4)
Problem 5 :
x-intercepts of 9 and 1; passes through (0, −18)
Problem 6 :
x-intercepts of −16 and −2; passes through (−18, 72)
Problem 7 :
Describe and correct the error in writing an equation of the parabola.
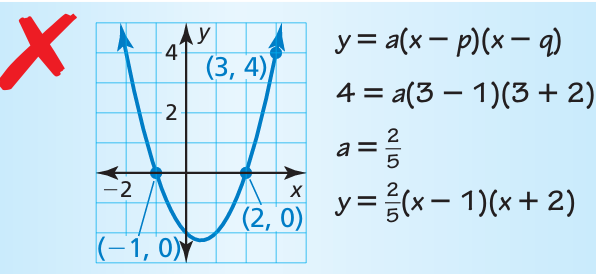
Answer Key
1) y = (1/2)(x2 + 8x + 12)
2) y = (-4/9)(x2 + 6x)
3) f(x) = 2(x + 1) (x - 2) So, option a is correct.
4) f(x) = (1/10)(x + 1) (x - 2)
5) f(x) = -2 (x - 9) (x - 1)
6) f(x) = 2.25 (x + 16) (x + 2)
7) y = 1(x + 1)(x - 2)
Problem 1 :
Form the equation whose roots are 1 and -5.
Problem 2 :
Form the equation whose roots are
(√3 - 2)/2 and (√3 + 2)/2
Problem 3 :
If 1 – i and 1 + i are the roots of the equation
x2 + ax + b = 0
where a, b ∈ r, then find the values of a and b.
Problem 4 :
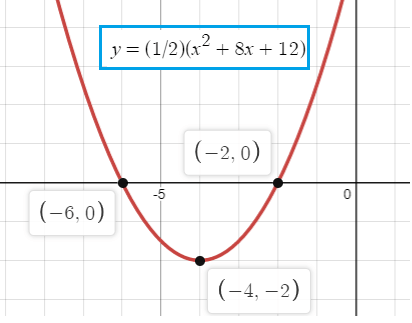
The roots of a quadratic equation are -2 and -6. The minimum point of the graph of its related function is at (-4, -2). Sketch the graph of the function.
Problem 5 :
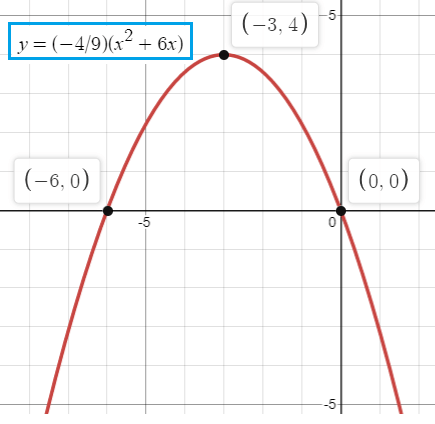
The roots of a quadratic equation are -6 and 0. The minimum point of the graph of its related function is at (-3, 4). Sketch the graph of the function.
Problem 6 :
Which equations have roots that are equivalent to the x-intercepts of the graph shown?
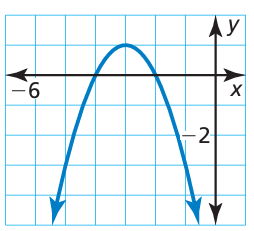
a) -x2 - 6x - 8 = 0 b) 0 = (x + 2)(x + 4) c) 0 = -(x + 2)2 + 4
d) 2x2 - 4x - 6 = 0 e) 4(x + 3)2 - 4 = 0
Answer Key
1) x2 + 4x - 5 = 0.
2) 4x2 - √3 x -1 = 0
3) a = -2 and b = 2
4) y = (1/2)(x2 + 8x + 12)
5) y = (-4/9)(x2 + 6x)
6) the intercepts are -2 and -4. so, option b and e are correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling