DETERMINE A QUADRATIC EQUATION GIVEN THE ROOTS AND A POINT

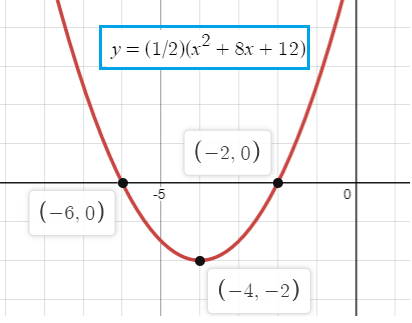
Problem 1 :

The roots of a quadratic equation are -2 and -6. The minimum point of the graph of its related function is at (-4, -2). Sketch the graph of the function.

Solution :

α = -2 and β = -6

α + β = -2 - 6 ==> -8

α β = -2 (-6) ==> 12

The quadratic function will be,

y = a(x² - (-8)x + 12)

y = a(x² + 8x + 12)

Since the quadratic function is having a minimum point (-4, -2), the will pass through this point.

-2 = a((-4)² + 8(-4) + 12)

-2 = a(16 - 32 + 12)

-2 = a(-4)

a = 1/2

By applying the value of a, we get

y = (1/2)(x² + 8x + 12)

So, the required quadratic function is

y = (1/2)(x² + 8x + 12)

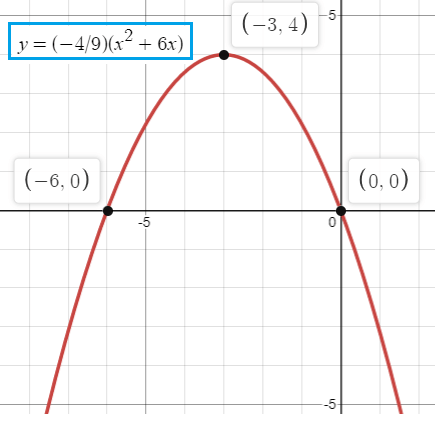
Problem 2 :

The roots of a quadratic equation are -6 and 0. The minimum point of the graph of its related function is at (-3, 4). Sketch the graph of the function.

Solution :

α = -6 and β = 0

α + β = -6 + 0 ==> -6

α β = -6 (0) ==> 0

The quadratic function will be,

y = a(x² - (-6)x + 0)

y = a(x² + 6x)

Since the quadratic function is having a minimum point (-3, 4), the will pass through this point.

4 = a((-3)² + 6(-3))

4 = a(9 - 18)

4 = a(-9)

a = -4/9

By applying the value of a, we get

y = (-4/9)(x² + 6x)

So, the required quadratic function is

y = (-4/9)(x² + 6x)