SOLVE SYSTEMS OF LINEAR EQUATIONS BY GRAPHING WORKSHEET

Find the simultaneous solution of the following pairs of equations using graphical methods:

Problem 1 :

y = x + 1

y = 2x - 3

Solution

Problem 2 :

y = x + 4

y = -x + 2

Solution

Problem 3 :

y = x + 2

y = -2x + 5

Solution

Problem 4 :

y = 2x - 2

y = 1 - x

Solution

Problem 5 :

Describe and correct the error in solving the system of linear equations.

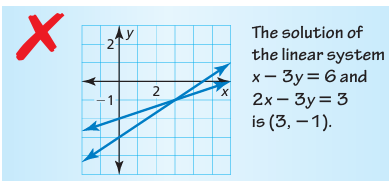
Problem 6 :

Describe and correct the error in solving the system of linear equations.

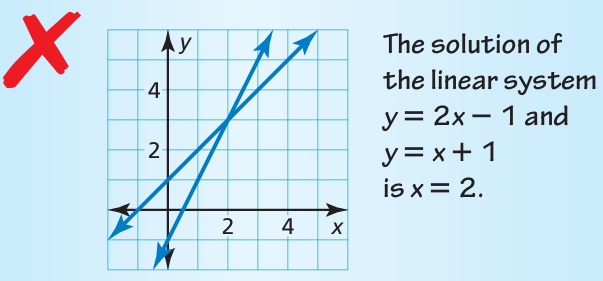
Answer key

1) Solution is (4, 5)

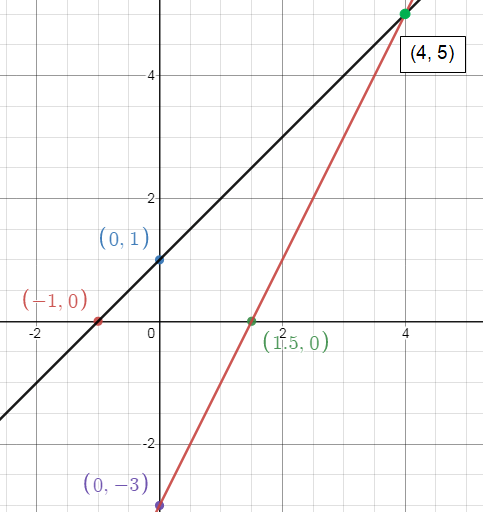
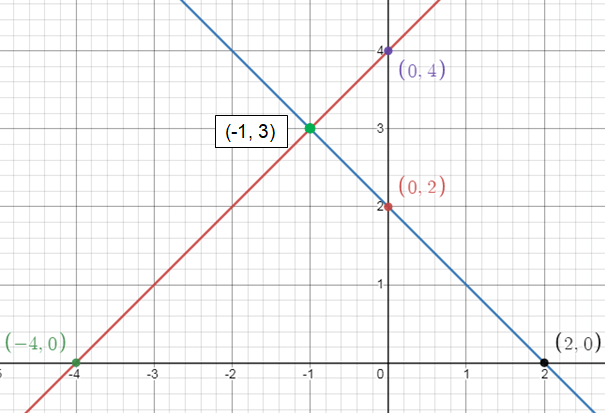
2) Solution is (-1, 3)

3) Solution is (1, 3)

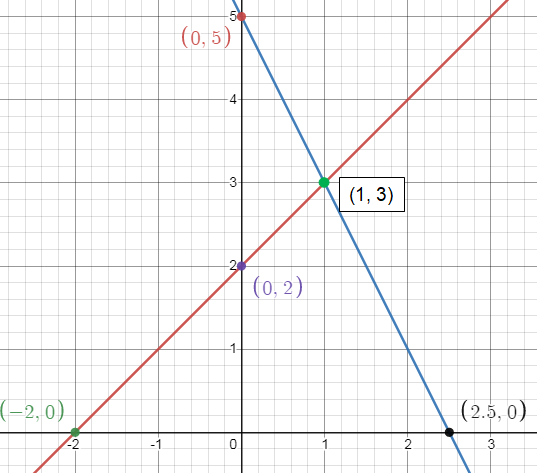
4) Solution is (1, 0)

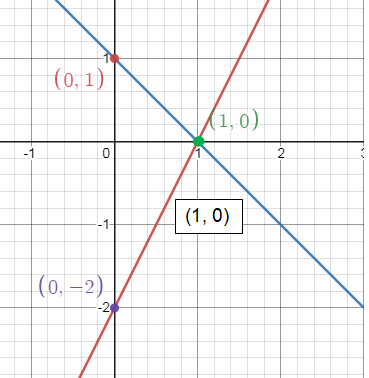
5) The solution should be (-3, -3). But observing the graph it says (3, -1) is the solution and that is the error.

6) , the solution should be (2, 3).

Problem 1 :

y = 3x - 1

y = 2x - 2

Solution

Problem 2 :

y = -2x + 3

y = x + 6

Solution

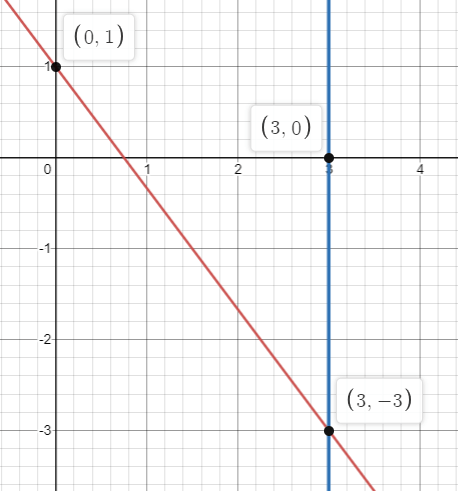
Problem 3 :

y = -(4/3)x + 1

x = 3

Solution

Problem 4 :

2x - 5y = a

bx + 10y = -8

In the given system of equations a and b are constants. If the system has infinitely many solutions, what is the value of a ?

a)  -4    b)  1/4     c)   4     d)  16

Solution

Problem 5 :

-5x = 8 - ky

18y + 5x = -10x + 21

In the given system of equations, k is a constant. If the system has no solution, what is the value of k ?

Solution

Problem 6 :

9(2x + 1) + 27(y - 4) = 810

(2x + 1) + (y - 4) = -393

The solution to the given system of equations is (x, y). What is the value fo 8(y - 4) ?

Solution

Answer Key

1) Solution is (-1, -4)

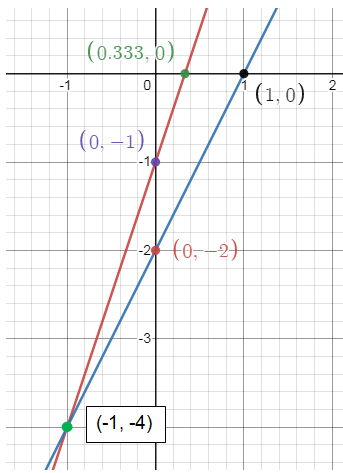
2) Solution is (-1, 5)

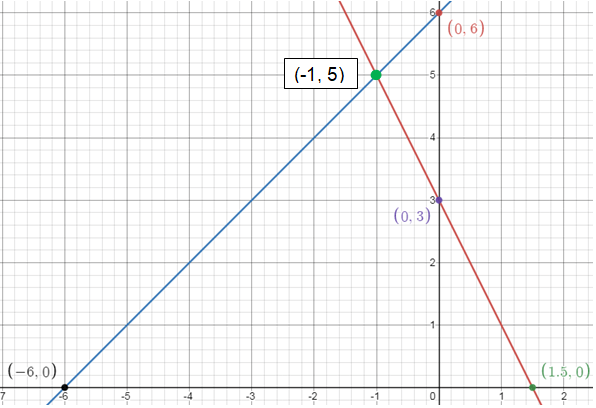
3) Solution is (3, -3)

4) a = 4

5) k = -6

6) 1932

Problem 1 :

For what value of k the pair of equations

x + (k + 1) y = 5

(k + 1)x + 9y = 8k - 1

has infinitely many solutions.

Solution

Problem 2 :

Find the value of k for which the pair of equations

2x + 3y = 7

(k - 1)x + (k + 2)y = 3k

has infinitely many solutions.

Solution

Problem 3 :

For what value of k the pair of equations

kx + 2y = 5

3x - 4y = 10

has no solution.

Solution

Problem 4 :

For what value of k the pair of equations

3x + y = 1

(2k - 1)x + (k - 1)y = (2k + 1)

has no solution.

Solution

Problem 5 :

Show that the system of equations

3x + 4y = 8

6x + 8y = 10

is inconsistent.

Solution

Problem 6 :

For what value of k for which the pair of equations.

2x + 5y = 0

kx + 10y = 0

has a non zero solution.

Solution

Problem 1 :

For what value of c will the system of equations below have no solution ?

cx - 2y = 6

3x + 4y = 4

Solution

Problem 2 :

For what value of b will the system of equations below have infinitely many solution ?

-2x + y = 4

5x - by = -10

Solution

Problem 3 :

ax - y = 0

x - by = 1

In the system of equations above, a and b are constants and x and y are variables. If the system of equations above has no solution. What is the value of a ⋅ b ?

Solution

Problem 4 :

2x - ky = 14

5x - 2y = 5

In the system of equations above, k is constant and x and y are variables. For what values of k will the system of equations have no solution ?.

Solution

Without graphing, determine whether the system of linear equations has one solution, infinitely many solutions, or no solution. Explain your reasoning.

Problem 5 :

y = 5x - 9

y = 5x + 9

Solution

Problem 6 :

y = 6x + 2 

y = 3x + 1

Solution

Problem 7 :

y = 8x - 2

y - 8x = -2

Solution