SOLVE SYSTEMS OF EQUATIONS BY GRAPHING

Find the simultaneous solution of the following pairs of equations using graphical methods:

Problem 1 :

y = 3x - 1

y = 2x - 2

Solution :

y = 3x - 1

By connecting these two points, we get the first line.

y = 2x - 2

By connecting these two points, we get the second line.

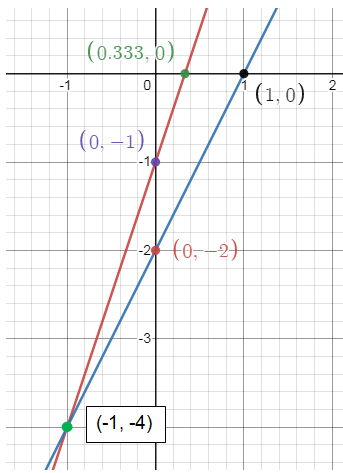
In the graph, the lines are intersecting at a point (-1, -4).

So, the solution is (-1, -4).

Problem 2 :

y = -2x + 3

y = x + 6

Solution :

y = -2x + 3

By connecting these two points, we get the graph of the first line.

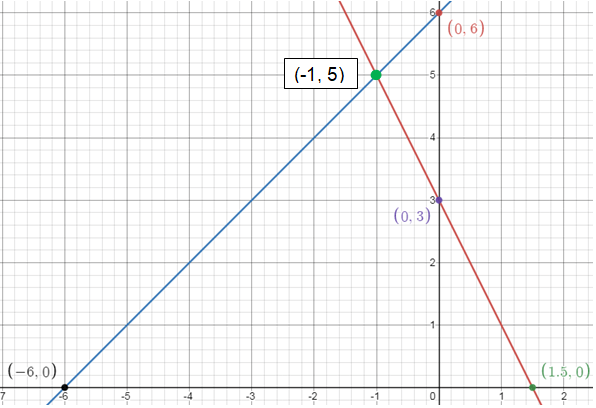
So, the solution is (-1, 5).

Problem 3 :

y = -(4/3)x + 1

x = 3

Solution :

y = -(4/3) x + 1

By connecting the points (3/4, 0) and (0, 1), we get the graph of the first line.

The second line is x = 3, it is vertical line passes through 3 on  the x-axis.

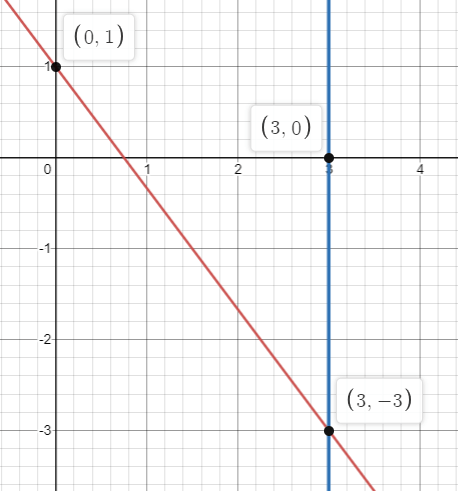
So, (3, -3) is the solution.

Problem 4 :

2x - 5y = a

bx + 10y = -8

In the given system of equations a and b are constants. If the system has infinitely many solutions, what is the value of a ?

a)  -4    b)  1/4     c)   4     d)  16

Solution :

2x - 5y = a ----(1)

bx + 10y = -8 ----(2)

Given that the system has infinitely many solution, then their slopes and y-intercepts will be equal. 

From (1),

5y = 2x - a

y = (2/5)x - (a/5)

Slope (m₁) = 2/5 and y-intercept (b₁) = -a/5

From (2),

10y = -bx - 8

y = (-b/10)x - (8/10)

y = (-b/10)x - (4/5)

Slope (m₂) = -b/10 and y-intercept (b₂) = -4/5

-a/5 = -4/5

By comparing the numerators, we get a = 4. Option c is correct.

Problem 5 :

-5x = 8 - ky

18y + 5x = -10x + 21

In the given system of equations, k is a constant. If the system has no solution, what is the value of k ?

Solution :

Given that, the system has no solution. Then there must be no point of intersection and they will have same slope and same y-intercept.

-5x = 8 - ky -----(1)

18y + 5x = -10x + 21 -----(2)

From (1),

ky = 5x + 8

y = (5/k) x + (8/k)

Slope (m₁) = 5/k and y-intercept (b₁) = 8/k

From (2),

10x + 5x + 18y = 21

15x + 18y = 21

Dividing by 3, we get

5x + 6y = 7

6y = -5x + 7

y = (-5/6)x + (7/6)

Slope (m₂) = -5/6 and y-intercept (b₂) = 7/6

5/k = -5/6

k = -6

So, the value of k is -6.

Problem 6 :

9(2x + 1) + 27(y - 4) = 810

(2x + 1) + (y - 4) = -393

The solution to the given system of equations is (x, y). What is the value fo 8(y - 4) ?

Solution :

9(2x + 1) + 27(y - 4) = 810 ----(1)

(2x + 1) + (y - 4) = -393 -----(2)

Without expanding the equations, let us multiply the second equation by9 and subtract.

9(2x + 1) + 27(y - 4) - [9(2x + 1) + 9(y - 4)]  = 810 - 9(-393)

9(2x + 1) + 27(y - 4) - 9(2x + 1) - 9(y - 4)  = 810 + 3537

18(y - 4)  = 810 + 3537

18(y - 4)  = 4347

(y - 4) = 4347/18

8(y - 4) = 8(241.5)

8(y - 4) = 1932

So, the value of 8(y - 4) is 1932.