RATIONAL FUNCTIONS AND ASYMPTOTES

Asymptotes are lines that the curve approaches at the edges of the coordinate plane. 

Types of asymptotes :

• Horizontal asymptote
• Vertical asymptote
• Oblique or slant asymptote

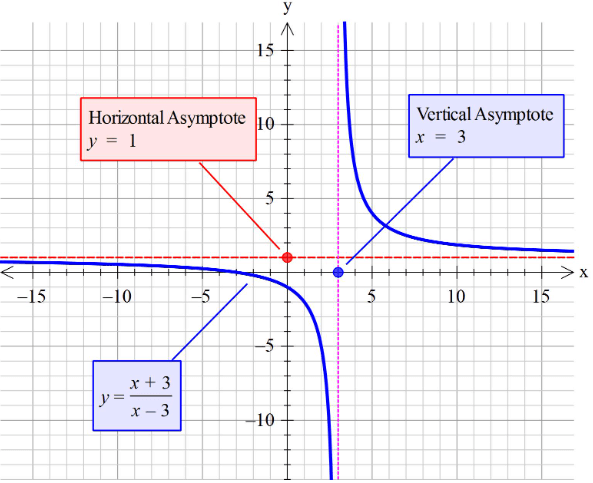
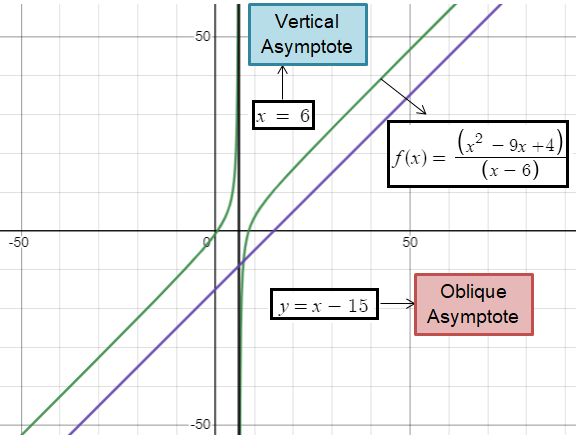
Find the horizontal asymptote of the graph of each rational function.

Problem 1 :

y = 2/(x – 6)

Solution :

 y = 2/(x – 6)

Degree of numerator = 0

Degree of denominator = 1

degree of numerator < degree of denominator

So, equation of the horizontal asymptote is y = 0 which is the x – axis.

Problem 2 :

y = (x + 2)/(x – 4)

Solution :

y = (x + 2)/(x – 4)

Degree of numerator = 1

Degree of denominator = 1

degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

So, equation of the horizontal asymptote is y = 1.

More problems on horizontal asymptotes

Describe the vertical asymptotes and holes for the graph of each rational function.

Problem 3 :

y = (x - 2)/(x + 2) (x - 2)

Solution :

y = (x - 2)/(x + 2) (x - 2)

We see x – 2 as a common factor in both numerator and denominator.

After cancel x – 2. We get,

1/(x + 2)

To find vertical asymptote, we equate the denominator to 0.

x + 2 = 0

x = -2

We see the hole at x = 2 in the graph.

x – 2 = 0 we will get hole at x = 2.

So, the vertical asymptote at x = -2; hole at x = 2.

More problems on vertical asymptotes

Find the oblique asymptote of the rational function

Problem 4 :

f(x) = (x² + 8x – 20)/(x – 1)

Solution :

f(x) = (x² + 8x – 20)/(x – 1)

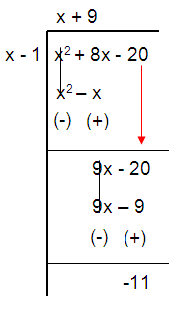
y = (x + 9) -11/(x – 1)

So, the oblique asymptote of the rational function is

y = x + 9

More problems on oblique asymptotes