FINDING OBLIQUE ASYMPTOTES OF RATIONAL FUNCTIONS

A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.

To find the slant asymptote you must divide the numerator by the denominator using either long division or synthetic division.

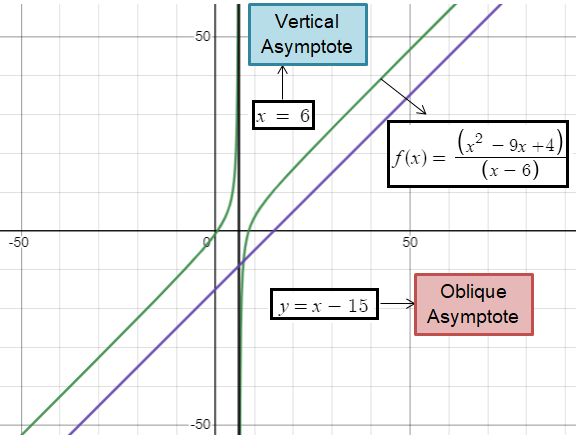
Find the oblique asymptote of the rational function

Problem 1 :

f(x) = (x² + 8x – 20)/(x – 1)

Solution :

Given, f(x) = (x² + 8x – 20)/(x – 1)

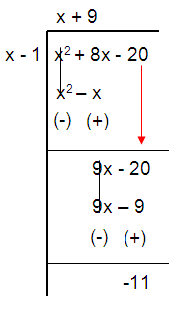
y = (x + 9) -11/(x – 1)

So, the oblique asymptote of the rational function is

y = x + 9

Find the oblique asymptote of the rational functions :

Problem 2 :

f(x) = (6x³ – 1)/(-2x² + 18)

Solution :

f(x) = (6x³ – 1)/(-2x² + 18)

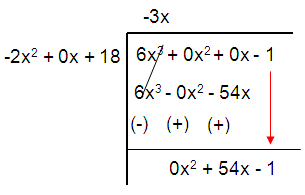
y = -3x + (0x² + 54x – 1)/(-2x² + 0x + 18)

So, the oblique asymptote of the rational function is

y = -3x.

Problem 3 :

f(x) = (2x² + x – 5)/(x + 1)

Solution :

f(x) = (2x² + x – 5)/(x + 1)

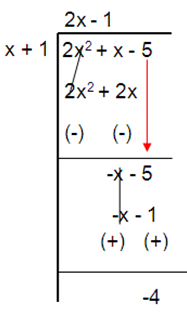
y = (2x – 1) + (-4)/(x + 1)

So, the oblique asymptote of the rational function is

y = 2x - 1

Problem 4 :

f(x) = (2x² - 5x + 3)/(x – 1)

Solution :

f(x) = (2x² - 5x + 3)/(x – 1)

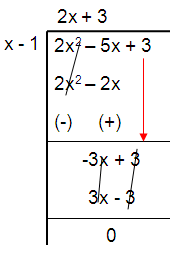
y = (2x + 3) + 0/(x - 1)

So, the oblique asymptote of the rational function is

y = 2x + 3

Problem 5 :

f(x) = (2x² - 5x + 5)/(x – 2)

Solution :

f(x) = (2x² - 5x + 5)/(x – 2)

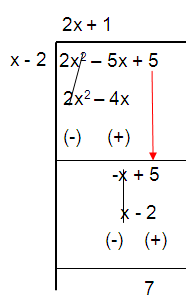
y = (2x + 1) + 7/(x - 2)

So, the oblique asymptote of the rational function is

y = 2x + 1

Problem 6 :

f(x) = (x³ - 2x² + 5)/x²

Solution :

f(x) = (x³ - 2x² + 5)/x²

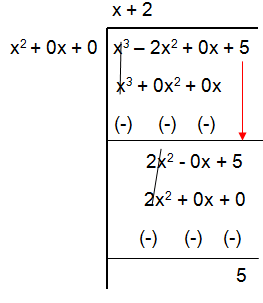
y = (x + 2) + 5/x²

So, the oblique asymptote of the rational function is

y = x + 2

Identify the vertical and oblique asymptotes of the following rational function.

Problem 7 :

f(x) = (x³ - x² - x - 1)/(x – 3) (x + 4)

Solution :

f(x) = (x³ - x² - x - 1)/(x – 3) (x + 4)

x – 3 = 0

x = 3

x + 4 = 0

x = -4

Vertical asymptotes at x = 3 and -4.

f(x) = (x³ - x² - x - 1)/(x – 3) (x + 4)

= (x³ - x² - x - 1)/(x² + 4x – 3x – 12)

f(x) = (x³ - x² - x - 1)/(x² + x – 12)

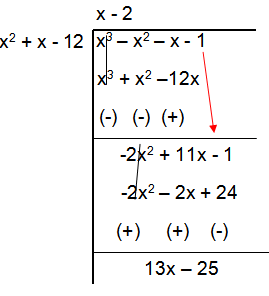
f(x) = (x – 2) + 13x – 25/(x² + x – 12)

So, the oblique asymptote of the rational function is

y = x – 2.

Find the asymptotes and intercepts of the function:

Problem 8 :

f(x) = x³/(x² – 4)

Solution :

f(x) = x³/(x² – 4)

Horizontal Asymptote :

Degree of numerator > degree of denominator

So, there is no horizontal asymptotes.

Vertical asymptote :

x² – 4 = 0

(x + 2) (x – 2) = 0

x + 2 = 0 and x – 2 = 0

x = -2 x = 2

Vertical asymptotes at x = -2 and 2.

Oblique asymptote :

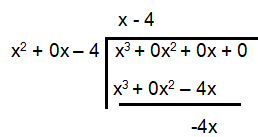
Oblique asymptote is at y = x-4.

x – intercept :

x – intercepts occurs when y = 0.

f(x) = x³

0 = x³

x = 0

So, the x – intercepts is (0, 0).

y – intercept :

y – intercepts occurs when x = 0.

f(x) = 0/(0 – 4)

f(0) = 0/4

f(0) = 0

So, the y – intercepts is (0, 0).