QUADRATIC FUNCTIONS AND EQUATION REVIEW WORKSHEET

Problem 1 :

The function f(t) = -5t² + 20t + 60 models the approximate height of an object t seconds after it is launched. How many seconds does it take the object to hit the ground?

Solution

Problem 2 :

What is the smallest of 3 consecutive positive integers if the product of the smaller two integers is 5 less than 5 times the largest integer?

Solution

Problem 3 :

The larger leg of a right triangle is 3 cm longer than its smaller leg. The hypotenuse is 6 cm longer than the smaller leg. How many centimeters long is the smaller leg?

Solution

Problem 4 :

Which term is a factor of 3a² + 12a?

A. 3a B. 4a C. 3a²D. 4a²

Solution

Problem 5 :

Which graph displays function f(x) = (2x + 3) (x - 2)?

Solution

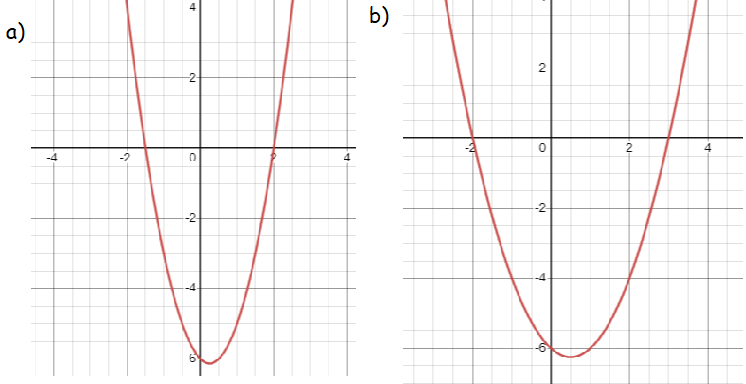
Problem 6 :

The floor of a rectangular cage has a length 4 feet greater than its width, w. James will increase both dimensions of the floor by 2 feet. Which equation represents the new area, N, of the floor of the cage?

A. N = w² + 4w B. N = w² + 6w C. w² + 6w + 8

D. w² + 8w + 12

Solution

Problem 7 :

Which expression is equivalent to t² - 36?

A. (t - 6)(t - 6) B. (t + 6)(t - 6)

C. (t - 12)(t - 3) D. (t - 12)(t +3)

Solution

Problem 8 :

Draw the graph of the function f(x) = 4x² - 8x + 7?

Solution

Problem 9 :

Suppose that the equation V = 20.8x² - 458.3x + 3,500 represents the value of a car from 1964 to 2002. What year did the car have the least value? (x = 0 in 1964)

A. 1965 B. 1970 C. 1975 D. 1980

Solution

Problem 10 :

The number of bacteria in a culture can be modeled by the function N(t) = 28t² - 30t + 160, where t is the temperature, in degrees Celsius, the culture is being kept. A scientist wants to have fewer than 200 bacteria in a culture in order to test a medicine effectively. What is the approximate domain of temperatures that will keep the number of bacteria under 200?

A. -1.01°C < t < 2.03°C B. -0.90°C < t < 1.97°C

C. -0.86°C < t < 1.93°C D. -0.77°C < t < 1.85°C

Solution

Problem 11 :

Which equation has exactly one real solution?

A. 4x² - 12x - 9 = 0 B. 4x² + 12x + 9 = 0

C. 4x² - 6x - 9 = 0 D. 4x² + 4x + 9 = 0

Solution

Problem 12 :

The sum of two numbers is 24. The sum of the squares of the two numbers is 306. What is the product of the two numbers?

A. 119 B. 128 C. 135 D. 144

Solution

Problem 13 :

The heights of two different projectiles after they are launched are modeled by f(x) and g(x). The function f(x) is defined as f(x) = -16x² + 42x + 12. The table contains the values for the quadratic function g.

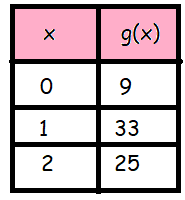
What is the approximate difference in the maximum heights achieved by the two projectiles?

A. 0.2 feet B. 3.0 feet C. 5.4 feet D. 5.6 feet

Solution

Problem 14 :

Which expression is equivalent to -3x(x - 4) - 2x(x + 3)?

(A) -x² - 1 (B) -x² + 18x (C) -5x² - 6x (D) -5x² + 6x

Solution

Problem 15 :

The length f a rectangle is 3 inches more than its width. The area of the rectangle is 40 square inches. What is the length, in inches, of the rectangle?

(A) 5 (B) 8 (C) 8.5 (D) 11.5

Solution

Problem 16 :

Which expressions represents 36x² - 100y⁶ factored completely?

(A) 2(9x + 25y³)(9x - 25y³) (B) 4(3x + 5y³)(3x - 5y³)