QUADRATIC EQUATIONS AND FUNCTIONS REVIEW

Problem 1 :

The function f(t) = -5t² + 20t + 60 models the approximate height of an object t seconds after it is launched. How many seconds does it take the object to hit the ground?

Solution:

f(t) = -5t² + 20t + 60

= 5t² - 20t - 60

Dividing by 5

t² - 4t - 12 = 0

t² - 6t + 2t - 12 = 0

t(t - 6) + 2(t - 6) = 0

(t + 2) (t - 6) = 0

As time cannot be negative, the object will hit the ground after 6 seconds.

Problem 2 :

What is the smallest of 3 consecutive positive integers if the product of the smaller two integers is 5 less than 5 times the largest integer?

Solution:

Let the smallest number be x, and the second and third be x + 1 and x + 2.

x(x + 1) = 5(x + 2) - 5

x² + x = 5x + 10 - 5

x² - 4x - 5 = 0

(x - 5) (x + 1) = 0

x = 5 and x = -1

The numbers have to be positive, the smallest number is 5.

x + 1 = 5 + 1 = 6

x + 2 = 5 + 2 = 7

So, the 3 consecutive integers are 5, 6 and 7.

Problem 3 :

The larger leg of a right triangle is 3 cm longer than its smaller leg. The hypotenuse is 6 cm longer than the smaller leg. How many centimeters long is the smaller leg?

Solution:

Let x represent the shorter leg.

Then the length of the longer will be x + 3 and

the length of the hypotenuse will be x + 6.

By using Pythagorean Theorem,

x² + (x + 3)² = (x + 6)²

x² + x² + 6x + 9 = x² + 12x + 36

2x² - x² + 6x - 12x + 9 - 36 = 0

x² - 6x - 27 = 0

(x - 9) (x + 3) = 0

x = 9 or x = -3

The length can't be negative. 

So, x = 9

The length of the shorter leg is 9 centimeters.

Problem 4 :

Which term is a factor of 3a² + 12a?

A. 3a        B. 4a          C. 3a²            D. 4a²

Solution:

= 3a² + 12a

= 3a(a + 4)

So, option (A) is correct.

Problem 5 :

Which graph displays function f(x) = (2x + 3) (x - 2)?

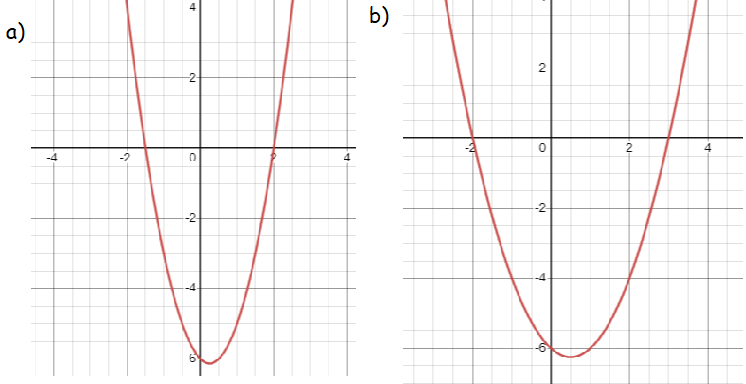
Solution:

f(x) = (2x + 3)(x - 2)

x-intercept : put y = 0

Converting into vertex form :

f(x) = (2x + 3)(x - 2)

f(x) = 2x² - 4x + 3x - 6

f(x) = 2x² - x - 6

f(x) = 2[x² - (1/2)x] - 6

f(x) = 2[x² - (1/2)x] - 6

So, graph (a) is correct.

Problem 6 :

The floor of a rectangular cage has a length 4 feet greater than its width, w. James will increase both dimensions of the floor by 2 feet. Which equation represents the new area, N, of the floor of the cage?

A. N = w² + 4w       B. N = w² + 6w        C. w² + 6w + 8

D. w² + 8w + 12

Solution:

Given, the original width = w

The original length = w + 4

Both length and width will be increased by 2 feet

So, new length = w + 6, new width = w + 2

New area N = (w + 6) (w + 2)

= w² + 2w + 6w + 12

N = w² + 8w + 12

So, option (D) is correct.

Problem 7 :

Which expression is equivalent to t² - 36?

A. (t - 6)(t - 6)         B. (t + 6)(t - 6)

C. (t - 12)(t - 3)         D. (t - 12)(t +3)

Solution:

= t² - 36

= t² - 6²

(t + 6) (t - 6)

So, option (B) is correct.

Problem 8 :

Draw the graph of the function f(x) = 4x² - 8x + 7?

Solution:

f(x) = 4x² - 8x + 7

Let us find vertex and zeroes of the quadratic function.

f(x) = 4[x² - 2x] + 7

f(x) = 4[(x - 1)² - 1] + 7

= 4(x - 1)² - 4 + 7

= 4(x - 1)² + 3

y-intercept: x = 0

f(x) = 7

y-intercept = (0, 7)

x-intercept: y = 0

4(x - 1)² + 3 = 0

Will get unreal value, so there is x-intercepts.

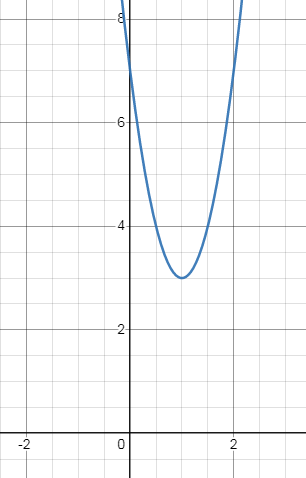
So, option (D) is correct.

Problem 9 :

Suppose that the equation V = 20.8x² - 458.3x + 3,500 represents the value of a car from 1964 to 2002. What year did the car have the least value? (x = 0 in 1964) 

A. 1965     B. 1970       C. 1975       D. 1980

Solution:

V = 20.8x² - 458.3x + 3500

To find the least value, we can figure out the minimum value.

x = -b/2a

x = 458.3/2(20.8)

When V' = 0, it has least value

41.6x - 458.3 = 0

41.6x = 458.3

x = 458.3/41.6

x = 11.01

1964 + 11 = 1975

So, option (C) is correct.

Problem 10 :

The number of bacteria in a culture can be modeled by the function N(t) = 28t² - 30t + 160, where t is the temperature, in degrees Celsius, the culture is being kept. A scientist wants to have fewer than 200 bacteria in a culture in order to test a medicine effectively. What is the approximate domain of temperatures that will keep the number of bacteria under 200?

A. -1.01°C < t < 2.03°C        B. -0.90°C < t < 1.97°C

C. -0.86°C < t < 1.93°C        D. -0.77°C < t < 1.85°C

Solution:

 N(t) = 28t² - 30t + 160

200 = 28t² - 30t + 160

28t² - 30t - 40 = 0

By using quadratic formula,

a = 28

b = -30

c = -40

-0.77°C < t < 1.85°C

So, option (D) is correct