QUADRATIC FUNCTIONS AND EQUATIONS PRACTICE PROBLEMS

Problem 11 :

Which equation has exactly one real solution?

A. 4x² - 12x - 9 = 0       B. 4x² + 12x + 9 = 0

C. 4x² - 6x - 9 = 0         D. 4x² + 4x + 9 = 0

Solution:

A general quadratic equation can be represented as

ax² + bx + c = 0

A. 

D = b² - 4ac

4x² - 12x - 9 = 0

D = (-12)² - 4(4)(-9)

= 144 + 144 = 288

D > 0

So, equation have two real and distinct solutions.

B.

D = b² - 4ac

4x² + 12x + 9 = 0

D = (12)² - 4(4)(9)

= 144 - 144

D = 0

So, equation has exactly one real solution.

So, option (B) is correct.

Problem 12 :

The sum of two numbers is 24. The sum of the squares of the two numbers is 306. What is the product of the two numbers?

A. 119           B. 128         C. 135         D. 144

Solution:

x + y = 24 ---> (1)

x² + y² = 306 ---> (2)

Equation (1) squaring on both sides,

(x + y)² = 24²

x² + y² + 2xy = 576

306 + 2xy = 576

2xy = 576 - 306

2xy = 270

xy = 270/2

xy = 135

So, option (C) is correct.

Problem 13 :

The heights of two different projectiles after they are launched are modeled by f(x) and g(x). The function f(x) is defined as f(x) = -16x² + 42x + 12. The table contains the values for the quadratic function g. 

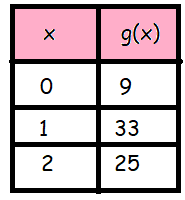
What is the approximate difference in the maximum heights achieved by the two projectiles?

A. 0.2 feet           B. 3.0 feet     C. 5.4 feet     D. 5.6 feet

Solution :

y = ax² + bx + c

The quadratic function passes through the points (0, 9) (1, 33) and (2, 25) respectively.

By applying the point (0, 9), we get

9 = a(0)² + b(0) + c

c = 9

By applying the point (1, 33), we get

33 = a(1)² + b(1) + 9

33 = a + b + 9

a + b = 33 - 9

a + b = 24 ----(1)

By applying the point (2, 25), we get

25 = a(2)² + b(2) + 9

25 - 9 = 4a + 2b

4a + 2b = 16

2a + b = 8 ----(2)

(1) - (2)

-a = 16, a = -16

b = 24 + 16

b = 40

So, the required equation is g(x) = -16x² + 40x + 9

Calculating the maximum value of f(x) :

f(x) = -16x² + 42x + 12

x = -b/2a

x = 42/32

x = 1.31

f(1.31) = -16(1.31)² + 42(1.31) + 12

f(1.31) = 39.56 

Calculating the maximum value of g(x) :

g(x) = -16x² + 40x + 9

x = -b/2a

x = 40/32

x = 1.25

g(1.25) = -16(1.25)² + 40(1.25) + 9

g(1.25) = 34

f(1.31) - g(1.25) =  5.56 ft

So, approximately 5.6 ft. Option D.

Problem 14 :

Which expression is equivalent to -3x(x - 4) - 2x(x + 3)?

(A) -x² - 1        (B) -x² + 18x         (C) -5x² - 6x     (D) -5x² + 6x

Solution:

= -3x(x - 4) - 2x(x + 3)

= -3x² + 12x - 2x² - 6x

= -5x² + 6x

So, option (4) is correct.

Problem 15 :

The length f a rectangle is 3 inches more than its width. The area of the rectangle is 40 square inches. What is the length, in inches, of the rectangle?

(A) 5        (B) 8         (C) 8.5         (D) 11.5

Solution:

Given A = 40 in²

l = w + 3

Area = l × w

40 = (w + 3) × w

40 = w² + 3w

w² + 3w - 40 = 0

(w + 8) (x - 5) = 0

w = -8 or w = 5

Since length can't be in negative.

length = w + 5

= 5 + 3

length = 8

So, option (2) is correct.

Problem 16 :

Which expressions represents 36x² - 100y⁶ factored completely?

(A) 2(9x + 25y³)(9x - 25y³)            (B) 4(3x + 5y³)(3x - 5y³)

(C) (6x + 10y³)(6x - 10y³)             (D) (18x + 50y³)(18x - 50y³)

Solution:

= 36x² - 100y⁶

= 4(9x² - 25y⁶)

= 4[(3x)² - (5y³)²]

Using algebraic identity,

= 4(3x + 5y³)(3x - 5y³)

So, option (2) is correct.

Problem 17 :

What are the roots of the equation x² - 5x + 6 = 0?

(A) 1 and -6         (B) 2 and 3       (C) -1 and 6   (D) -2 and -3

Solution:

 x² - 5x + 6 = 0

 x² - 2x - 3x + 6 = 0

 x(x - 2) - 3(x - 2) = 0

 (x - 2)(x - 3) = 0

x - 2 = 0 and x - 3 = 0

x = 2 and x = 3

So, option (2) is correct.

Problem 18 :

Which expression is equivalent to 64 - x² ?

(A) (8 - x)(8 - x)       (B) (8 - x)(8 + x)    (C) (x - 8)(x - 8)

(D) (x - 8)(x + 8)

Solution:

= 64 - x²

= 8² - x²

Using algebraic identity,

(a² - b²) = (a - b)(a + b)

= (8 - x)(8 + x)

So, option (2) is correct.

Problem 19 :

The equation of the axis of symmetry of the graph of y = 2x² - 3x + 7 is

Solution:

y = 2x² - 3x + 7

a = 2

b = -3

c = 7

So, option (A) is correct.

Problem 20 :

The roots of the equation 3x² - 27x = 0 are

(A) 0 and 9      (B) 0 and -9          (C) 0 and 3      (D) 0 and -3

Solution:

3x² - 27x = 0

3x(x - 9) = 0

3x = 0 and x - 9 = 0

x = 0 and x = 9

So, option (A) is correct.