PROBLEMS ON DIAGONAL OF RECTANGLE WORKSHEET

Problem 1 :

The diagonal of the TV screen is 82 cm, and the height is 40 cm. Calculate the width of the screen.

Solution

Problem 2 :

The aspect ratio of the rectangle and its diagonal is 9 : 12 : 15. Calculate the area of the rectangle if the length of the diagonal is 105 cm.

Solution

Problem 3 :

There is a rectangle with the length of 12 cm and diagonal 8 cm longer than the width. Calculate the area of the rectangle.

Solution

Problem 4 :

The length of the sides of the rectangular garden are in the ratio 1 : 2. The connection of the centers of the adjacent sides is 20 m long. Calculate the perimeter of the rectangle.

Solution

Problem 5 :

The dimension of the rectangular plot are (x + 1) m and (2x - y)m. The sum of x and y is 3 m and the perimeter of the plots is 36 m. Find the area of the diagonal of the plot.

Solution

Problem 6 :

The diagonal of the rectangle given below is 36 m. Find the values of x and y.

Solution

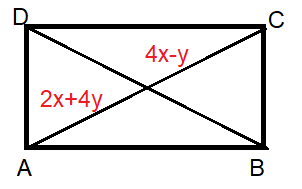
Problem 7 :

If the diagonal of a rectangle is 17 cm long and its perimeter is 46 cm, find the area of the rectangle.

Solution

Problem 8 :

A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is 

Problem 1 :

If the diagonal of a rectangle is 17 cm long and its perimeter is 46 cm, find the area of the rectangle.

Solution

Problem 2 :

One side of the rectangular field is 15 m and one of its diagonal is 17 m. Find the area of the field.

Solution

Problem 3 :

Find the area of square, one of whose diagonals is 3.8 m long.

Solution

Problem 4 :

Find the area of a rhombus one side of which measures 20 cm and one diagonal 24 cm.

Solution

Problem 5 :

One diagonal of a parallelogram is 70 cm and the perpendicular distance of this diagonal from either of the outlying vertices is 27 cm. The area of the parallelogram is.

Solution

Problem 6 :

If diagonal of one square is double the diagonal of another square, then find the ratio of their areas.

Solution

Problem 7 :

If length of diagonal of a square is 20 cm, then its perimeter is ________

Solution

Problem 8 :

If diagonal of a rectangle is thrice its smaller side, then find the ratio of its length and width.

Solution

Problem 9 :

The length of the diagonal of a square is 50. Find the perimeter of a square.

Solution

Problem 10 :

A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is

Solution

Problem 11 :

In rectangle QRST, QS = 5x − 31 and RT = 2x + 11. Find the lengths of the diagonals of QRST.

Solution

Problem 8 :

One side of the rectangular field is 15 m and one of its diagonal is 17 m. Find the area of the field.

Solution

Problem 9 :

Find the area of square, one of whose diagonals is 3.8 m long.

Solution

Problem 10 :

Find the area of a rhombus one side of which measures 20 cm and one diagonal 24 cm.

Solution

Problem 11 :

One diagonal of a parallelogram is 70 cm and the perpendicular distance of this diagonal from either of the outlying vertices is 27 cm. The area of the parallelogram is.

Solution

Problem 1 :

Find the diagonal of a square whose perimeter is 60 cm.

Solution

Problem 2 :

Perimeter of a rhombus is 146 cm and the length of one of its diagonals is 48 cm. Find the length of its other diagonal.

Solution

Problem 3 :

If diagonal of one square is double the diagonal of another square, then find the ratio of their areas.

Solution

Problem 4 :

If diagonal of a rectangle is thrice its smaller side, then find the ratio of its length and width.

Solution

Problem 5 :

A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is ____

Solution

Problem 6 :

If length of diagonal of a square is 20 cm, then its perimeter is _______

Solution

Problem 7 :

A square dinner napkin 8 in. on each side is folded along its diagonal. Find the area of the folder napkin.

Solution

Problem 8 :

What is the area of the rhombus ABCD, if AC = 6 cm, and BE = 4 cm?

Solution

Problem 9 :

find the value of each variable in the parallelogram.

Solution

Problem 10 :

Solution

Problem 11 :

The sides of ▱MNPQ are represented by the expressions below. Sketch ▱MNPQ and find its perimeter.

MQ = −2x + 37 QP = y + 14

Solution