PROBLEMS ON DIAGONALS OF 2D SHAPES

Problem 1 :

If the diagonal of a rectangle is 17 cm long and its perimeter is 46 cm, find the area of the rectangle.

Solution :

Let Length = x and width = y

Length of the diagonal = 17 cm

x² + y² = 17²

x² + y² = 289 ----(1)

Perimeter of the rectangle = 46 cm

2(x + y) = 46

Dividing by 2, we get

x + y = 23

Using the algebraic identity

a² + b² = (a + b)² - 2ab

x² + y² = (x + y)² - 2xy

Applying x² + y² in (1), we get

x² + y² = 289

(x + y)² - 2xy = 289

23² - 2xy = 289

529 - 289 = 2xy

240 = 2xy

xy = 120

So, area of the rectangle is 120 cm².

Problem 2 :

One side of the rectangular field is 15 m and one of its diagonal is 17 m. Find the area of the field.

Solution :

Length and width be the dimensions of the rectangle.

(Length)² + (width)² = (diagonal)²

Let length = 15 m

(15)² + (width)² = 17²

225 + (width)² = 289

(width)² = 289 - 225

Width = √64

width = 8 m

Area of the rectangle = 15(8)

= 120 m²

Problem 3 :

Find the area of square, one of whose diagonals is 3.8 m long.

Solution :

Since it is square, length of all sides will be equal.

a² + a² = (3.8)²

2a² = 14.44

a² = 7.22

So, area of the square is 7.22 m²

Problem 4 :

Find the area of a rhombus one side of which measures 20 cm and one diagonal 24 cm.

Solution :

In rhombus, the diagonals will bisect each other at right angle

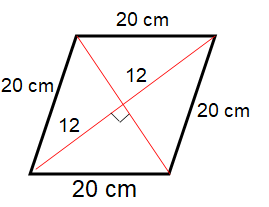
Let 2x be the length of the another diagonal. So, x be its half length.

12² + x² = 20²

144 + x² = 400

x² = 400 - 144

x² = 256

x = √256

x = 16 cm

Area of rhombus = (1/2) ⋅ 32 ⋅ 24

= 384 cm²

Problem 5 :

One diagonal of a parallelogram is 70 cm and the perpendicular distance of this diagonal from either of the outlying vertices is 27 cm. The area of the parallelogram is.

Solution :

The diagonal will divide the parallelogram into two triangles of equal area.

Base of the triangle = 70 cm

height of the triangle = 27 cm

Area of one triangle =  (1/2) ⋅ 70 ⋅ 27

= 945 cm²

Area of parallelogram = 2(945)

= 1800 cm²

Problem 6 :

If diagonal of one square is double the diagonal of another square, then find the ratio of their areas .

Solution :

Let d₁ and d₂ be the lengths of diagonal of two squares.

d₁ = 2d₂

Let x be the side length of square.

x² + x² = d₁²

2x² = d₁²

x² = (1/2)d₁²

Area of square = (1/2)d₁²

= (1/2)d₁² : (1/2)d₂²

= (1/2)(2d₂)² : (1/2)d₂²

= (1/2)(4d₂²) : (1/2)d₂²

= 4 : 1

So, the required ratio is 4 : 1.

Problem 7 :

If length of diagonal of a square is 20 cm, then its perimeter is ________

Solution :

Length of the diagonal = 20cm

Let x be the side length of square.

x² + x² = 20²

2x² = 400

x² = 400/2

x² = 200

x = √200

x = 10√2

Perimeter = 4x

= 4(10√2)

= 40√2

Problem 8 :

If diagonal of a rectangle is thrice its smaller side, then find the ratio of its length and width.

Solution :

Let x be the length of the rectangle and y be the width of the rectangle.

Smaller side = y and longer side = x.

diagonal = 3y

(3y)² = y² + x²

9y² = y² + x²

9y² - y² = x²

8y² = x²

x² /y² = 8/1

(x/y) = 2√2/1

x : y = 2√2 : 1

Problem 9 :

The length of the diagonal of a square is 50. Find the perimeter of a square .

Solution :

Length of diagonal = 50

Let x be the side length of square.

x² + x² = 50²

2x² = 2500

x² = 1250

x = √1250

= √(5 x 5 x 5 x 5 x 2)

= 5 x 5√2

= 25√2

Problem 10 :

A rectangular carpet has area 120 square meters and perimeter 46 meters. The length of its diagonal is

Solution :

Let x and y be the length and width of the rectangle.

xy = 120

2(x + y) = 46

x + y = 23

y = 23 - x

x(23 - x) = 120

23x - x² = 120

x² - 23x = -120

x² - 23x + 120 = 0

(x - 15)(x - 8) = 0

x = 15 and x = 8

Diagonal = √15² + 8²

= √(225 + 64)

= √289

= 17

So, the length of the diagonal is 17 meter.

Problem 11 :

In rectangle QRST, QS = 5x − 31 and RT = 2x + 11. Find the lengths of the diagonals of QRST.

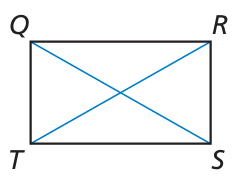
Solution :

Since it is a rectangle, the diagonals will be equal.

QS = RT

5x - 31 = 2x + 11

5x - 2x = 11 + 31

3x = 42

x = 42/3

x = 14

Length of the diagonal = 5(14) - 31

= 70 - 31

= 39 units