PRACTICE PROBLEMS ON PERPENDICULAR BISECTOR AND MEDIAN OF A TRIANGLE

Write an equation for the perpendicular bisector of the line segment joining

Problem 1 :

A(1, 4) and B(6, -6)

Solution

Problem 2 :

A(-3, -5) and B(9, -2)

Solution

Problem 3 :

A(5, 10) and B(10, 7)

Solution

Problem 4 :

For each of the following segments :

(i) Find the coordinates of the midpoint of the segment

(ii) Find the gradient of the segment

(iii) Find the equation of the perpendicular bisector of the segment.

Solution

Problem 1 :

A (-3, 4) and B (5, 6)

Solution

Problem 2 :

A (3, 8) and B (7, 14)

Solution

Problem 3 :

A (-5, 6) and B (1, 8)

Solution

Problem 4 :

A (-3, -6) and B (-1, 2)

Solution

The ordered pairs represent vertices of a triangle. Write an equation of the line containing the median that joins the first vertex to the side opposite it.

Problem 1 :

(8, 4), (0, 0), (10, 0)

Solution

Problem 2 :

(3, 10), (4, 2), (10, 8)

Solution

Problem 3 :

(2, 6), (3, 1), (7, 5)

Solution

Problem 4 :

A triangle has vertices A(-3, 7), B(4, -5), and C(9, -3). Determine the equation of the median from B.

Solution

Problem 5 :

A triangle has vertices Q(6, -4), R(5, 2), and S(1, 4). Determine the equation of the perpendicular bisector of QR.

Solution

Problem 1 :

Find the equation of the perpendicular bisector of P(9, 5) and Q(-1, 3).

Solution

Problem 2 :

Given that the triangle QRS have vertices (-3, 1), (-4, -2) and (7, 0).Find the equation of the perpendicular bisector of RS.

Solution

Problem 3 :

Pictured to the right is the straight line S1 and the points R and T.

(a) Find the equation of S1.

(b) S2 is perpendicular to S1 and passes through R. Find the equation of S2.

(c) Does S2 pass through T?

Solution

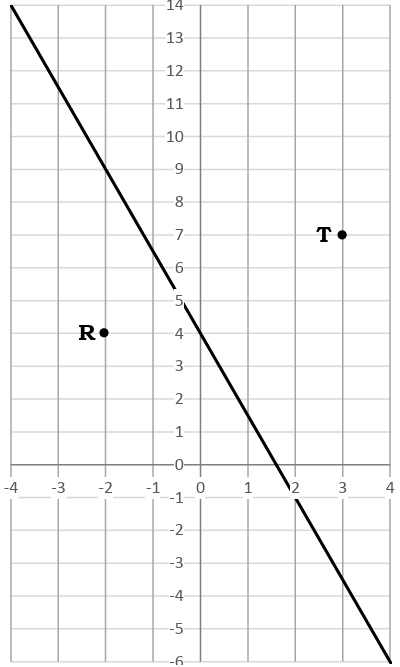
Problem 4 :

A = (-3, -2) B = (6, 4) The line C has equation 4y + 6x = 13. Show that C is perpendicular to AB.

Solution

Write the equation of the line which is perpendicular bisector to each pair of points.

Problem 1 :

A(-4, -2) and (8, 4)

(i) Midpoint

(ii) Slope of AB

(iii) Perpendicular slope

(iv) Equation of the line

Solution

Problem 2 :

A(-9, 11) and (-15,19)

(i) Midpoint

(ii) Slope of AB

(iii) Perpendicular slope

(iv) Equation of the line

Solution

Problem 3 :

A(11, -5) and (1, -10)

(i) Midpoint

(ii) Slope of AB

(iii) Perpendicular slope

(iv) Equation of the line

Solution

Problem 4 :

A(14, 18) and (-6, 10)

(i) Midpoint

(ii) Slope of AB

(iii) Perpendicular slope

(iv) Equation of the line

Solution

Problem 5 :

A triangle has vertices K(-2, -3), L(5, -7) and M(6, 1).

(a) Find the equation of the perpendicular bisector of the line KM.

(b) Show that the point L lies on this line.

(c) What kind of triangle is triangle KLM?

Solution