HOW TO FIND EQUATION OF PERPENDICULAR BISECTOR 

Problem 1 :

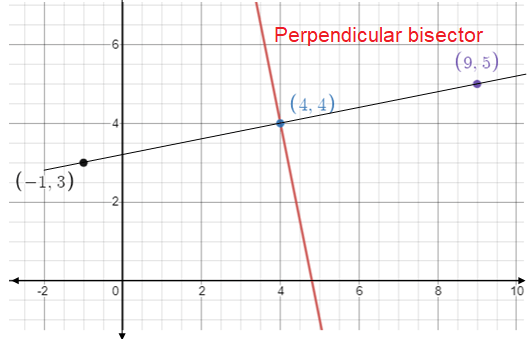
Find the equation of the perpendicular bisector of P(9, 5) and Q(-1, 3).

Solution :

Midpoint of the line segment PQ :

Midpoint = (x₁ + x₂)/2, (y₁ + y₂)/2

= (9 + (-1))/2, (5 + 3)/2

= 8/2, 8/2

= (4, 4)

Slope of the line joining the points P and Q :

m = (y₂ - y₁) / (x₂ - x₁)

m = (3 - 5)/(-1 - 9) 

m = -2/-10

m = 1/5

Slope of the perpendicular line = -1/(1/5) = -5

The perpendicular bisector is also a line which is perpendicular to the line joining the points P and Q and it will pass through the point (4, 4).

(y - y₁) = m(x - x₁)

y - 4 = -5(x - 4)

y - 4 = -5x + 20

y = -5x + 24

Problem 2 :

Given that the triangle QRS have vertices (-3, 1), (-4, -2) and (7, 0).Find the equation of the perpendicular bisector of RS.

Solution :

Let the vertices be Q(-3, 1), R(-4, -2) and S(7, 0)

Midpoint of the line joining the points RS :

midpoint = (x₁ + x₂)/2, (y₁ + y₂)/2

= (-4 + 7)/2, (-2 + 0)/2

= 3/2, -2/2

= (3/2, -1)

Slope of the line RS :

m = (0 + 2)/(7 + 4)

m = 2/11

Slope of the perpendicular bisector = -11/2

Equation of perpendicular bisector :

(y + 1) = (-11/2)(x - (3/2))

2(y + 1) = -11(x - (3/2))

2y + 2 = -11x + 33/2

2y = -11x + (33/2) - 2

2y = -11x + 29/2

y = (-11/2)x + (29/4)

Problem 3 :

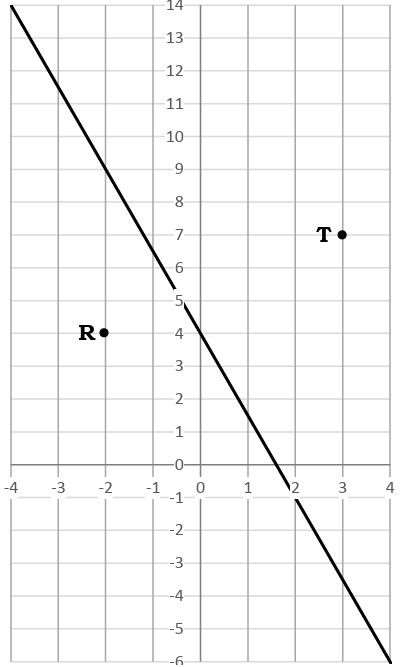
Pictured to the right is the straight line S1 and the points R and T.

(a) Find the equation of S1.

(b) S2 is perpendicular to S1 and passes through R. Find the equation of S2.

(c) Does S2 pass through T?

Solution :

a)  Equation of the line S1 shown :

Points on the line shown are (0, 4) and (-2, 9)

y-intercept = 4

Slope = (9 - 4) / (-2 - 0)

= 5/(-2)

= -5/2

y = (-5/2) x + 4

b) Slope of line S2 which is perpendicular to S1 = -1/(-5/2)

= 2/5

Equation of perpendicular line S2 passes through R :

T(-2, 4)

y - 4 = (2/5) (x - (-2)) 

5(y - 4) = 2(x + 2)

5y - 20 = 2x + 4

2x - 5y + 4 + 20 = 0

2x - 5y + 24 = 0

c) Check if the point T lies on the line :

T(3, 7)

Applying x = 3 and y = 7

2(3) - 5(7) + 24 = 0

6 - 35 + 24 = 0

-29 + 24 = 0

Since the point T does not satisfy the equation, T does not lie on the line S2.

Problem 4 :

A = (-3, -2) B = (6, 4) The line C has equation 4y + 6x = 13. Show that C is perpendicular to AB.

Solution :

6x + 4y = 13

4y = -6x + 13

y = (-6/4)x + (13/4)

y = (-3/2)x + (13/4)

Slope of the line C = -3/2

Slope of the line joining the points A = (-3, -2) B = (6, 4)

= (4 - (-2)) / (6 - (-3))

= (4 + 2) / (6 + 3)

= 6/9

= 2/3

Since the product of these two slopes is equal to -1. These two lines are perpendicular.

Problem 5 :

Line I passes through the points (5, 6) and (8, -3). Line J passes through the points (-2, -2) and (4, k). Lines I and J are perpendicular. Find k.

Solution :

Slope of the line joining the points (5, 6) and (8, -3).

= (-3 - 6) / (8 - 5)

= -9/3

= -3

Slope of the line L = -3

Slope of the line J passes through the points (-2, -2) and (4, k).

= (k - (-2)) / (4 - (-2))

= (k + 2) / (4 + 2)

= (k + 2) / 6

-3[(k + 2) / 6] = -1

3(k + 2) = 6

3k + 6 = 6

3k = 6 - 6

k = 0

So, the value of k is 0.