HOW TO FIND THE EQUATION OF A MEDIAN OF A TRIANGLE WITH VERTICES

A median of a triangle is a line segment joining a vertex and the midpoint of the opposite side.

Let ABC be the triangle, if we draw median from the vertex A, we follow the steps given below.

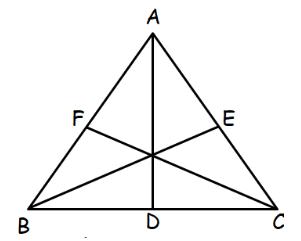
Step 1 :

Find the midpoint of the side BC. Name it as D.

Step 2 :

Using the points A and D, find the slope.

Step 3 :

Using the above slope and using one of the points A or D, we can find equation of the median AD.

For a triangle, maximum we can draw three medians. AD, BE and CF.

The ordered pairs represent vertices of a triangle. Write an equation of the line containing the median that joins the first vertex to the side opposite it.

Problem 1 :

(8, 4), (0, 0), (10, 0)

Solution :

A(8, 4), B(0, 0), C(10, 0)

Midpoint of BC :

= (x₁ + x₂)/2, (y₁ + y₂)/2

Substitute (x₁, y₁) = B(0, 0) and (x₂, y₂) = C(10, 0)

= (0 + 10)/2, (0 + 0)/2

= (10/2, 0)

= D(5, 0)

Slope of AD :

= (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = A(8, 4) and (x₂, y₂) = D(5, 0)

= (0 - 4)/(5 - 8)

= -4/-3

= 4/3

Equation of median AD :

y - y₁ = m(x - x₁)

Substitute (x₁, y₁) = A(8, 4) and m = 4/3

y - 4 = 4/3 (x - 8)

3(y - 4) = 4(x - 8)

3y - 12 = 4x - 32

4x - 3y - 32 + 12 = 0

4x - 3y - 20 = 0

Problem 2 :

(3, 10), (4, 2), (10, 8)

Solution :

A(3, 10), B(4, 2), C(10, 8)

Midpoint of BC :

= ((x₁ + x₂)/2, (y₁ + y₂)/2)

Substitute (x₁, y₁) = B(4, 2) and (x₂, y₂) = C(10, 8)

= (4 + 10)/2, (2 + 8)/2

= (14/2, 10/2)

= D(7, 5)

Slope of AD :

= (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = A(3, 10) and (x₂, y₂) = D(7, 5)

= (5 - 10)/(7 - 3)

= -5/4

Equation of median AD :

y - y₁ = m(x - x₁)

Substitute (x₁, y₁) = A(3, 10) and m = -5/4

y - 10 = -5/4 (x - 3)

4(y - 10) = -5(x - 3)

4y - 40 = -5x + 15

5x + 4y - 40 - 15 = 0

5x + 4y - 55 = 0

Problem 3 :

(2, 6), (3, 1), (7, 5)

Solution :

A(2, 6), B(3, 1), C(7, 5)

Midpoint of BC :

= ((x₁ + x₂)/2, (y₁ + y₂)/2)

Substitute (x₁, y₁) = B(3, 1) and (x₂, y₂) = C(7, 5)

= (3 + 7)/2, (1 + 5)/2

= (10/2, 6/2)

= D(5, 3)

Slope of AD :

= (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = A(2, 6) and (x₂, y₂) = D(5, 3)

= (3 - 6)/(5 - 2)

= -3/3

= -1

Equation of median AD :

y - y₁ = m(x - x₁)

Substitute (x₁, y₁) = A(2, 6) and m = -1

y - 6 = -1 (x - 2)

y - 6 = -x + 2

x + y - 6 - 2 = 0

x + y - 8 = 0