OPERATIONS WITH RADICALS WORKSHEET

Adding and subtracting radicals :

Problem 1 :

3√6 - 4√6

Solution

Problem 2 :

-3√7 + 4√7

Solution

Problem 3 :

-11√21 - 11√21

Solution

Problem 4 :

-9√15 + 10√15

Solution

Problem 5 :

-10√7 + 12√7

Solution

Problem 6 :

-3√17 - 4√17

Solution

Problem 7 :

-10√11 - 11√11

Solution

Problem 8 :

-2√3 + 3√27

Solution

Problem 9 :

2√6 - 2√24

Solution

Problem 10 :

2√6 + 3√54

Solution

Problem 11 :

-√12 + 3√3

Solution

Problem 12 :

3√3 - √27

Solution

Problem 13 :

3√8 + 3√2

Solution

Problem 14 :

-3√6 + 3√6

Solution

Find the perimeter of the shapes given below.

Problem 15 :

Solution

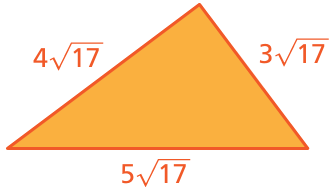
Problem 16 :

Solution

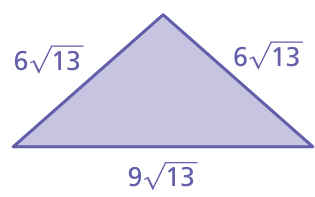
Problem 17 :

Solution

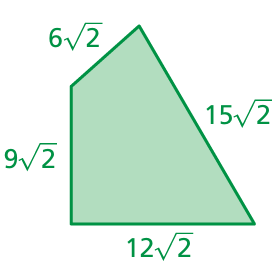
Problem 18 :

Solution

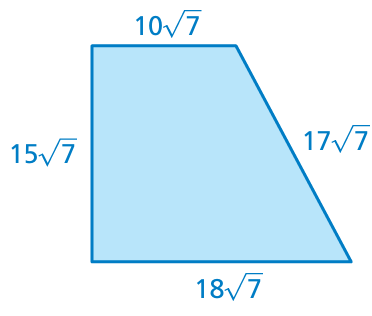
Problem 19 :

What are the perimeter and area of a rectangle with length of 5√3 cm and width of 3√2 cm ?

Solution

Problem 20 :

The sum of 2√8, 4√50 and 3√18 is

Solution

Problem 21 :

The difference between (1/2) √180 and (2/5) √20

Solution

Add or subtract. Assume all variables are positive. Answers must be simplified.

Problem 1 :

5√6 + 3√6

Solution

Problem 2 :

4√20 - 2√5

Solution

Problem 3 :

3√(32x²) + 5x√8

Solution

Problem 4 :

7√4x² + 2√25x - √16x

Solution

Problem 5 :

5∛x²y + ∛27x⁵y⁴ 

Solution

Problem 6 :

3√9y³ - 3y√16y + √25y³

Solution

Problem 7 :

√(248 + (√(51 + √169))

Solution

Problem 8 :

If a * b * c = √(a + 2) (b + 3) / (c + 1) then find the value of 6 * 15 * 3

Solution

Problem 9 :

What will come in the place of question mark in each of the following :

i)  √(32.4/?) = 2

ii)  √86.49 + √(5 + ?²) = 12

Solution

Problem 10 :

If √1 + (x/144) = 13/12, find the value of x

Solution

Problem 11 :

If x = 1 + √2 and y = 1 - √2, find the value of x² + y

Solution

Problem 12 :

√(10 + (√25 + (√108 + (√154 + (√225))))) is

Solution

Multiply the following radicals.

Problem 1 :

√6 × 4√6

Solution

Problem 2 :

-√5 × √20

Solution

Problem 3 :

-√2 × √3

Solution

Problem 4 :

4√8 × √2

Solution

Problem 5 :

√12×√15

Solution

Problem 6 :

√5 × (-2√5)

Solution

Problem 7 :

-3√5 ×√20

Solution

Problem 8 :

√15 × 3√5

Solution

Problem 9 :

√9 ×√3

Solution

Problem 10 :

 -4√8 ×√10

Solution

Problem 11 :

Express (√3 - √2)² in simplest form.

Problem 12 :

The radius of the circle is 3√5 cm. If a square is inscribed in a circle 

a) determine tehe exact length of the diagonal of a square

b)  Determine the exact perimeter of the square

Problem 13 :

The length of a rectangle is 2 √48 and width is 6√3. Express in the simplest form.

a) The area of the rectangle

b) The perimeter of the rectangle.

Problem 14 :

The area of the rectangle is 20√50 and length is 4√2, what is the width ?

Problem 15 :

If the perimeter of the rectangle is 12√3 and the length is 2√12, what is the width ?

Problem 16 :

The area of the parallelogram is 8√90 and the base is 2√5. What is the height of the parallelogram ?

1)  9³ x 27² = 3ⁿ, n = ?       Solution

2)  4^-a = 64, a = ?     Solution

3)  x^-3 = 1/8, x = ?     Solution

4)  5√8+7√32 = 

(a) 18√2  (b) 38√2  (c) 23√4  (d) 33√3  (e)  38√3

Solution

5)  4√18 x 11√12 = 

(a) 12√6  (b) 34√6  (c) 264√6  (d) 264√3  (e)  264√2

Solution

6)  y^-5 = 1024, y = ?        Solution

7)  2^-n = 1/256, n = ?             Solution

8)  √x = 4a²bc³, x = ?      Solution

9)  8¹² = 2^x, x = ?          Solution

10)  c^2/5 = 4, c = ?            Solution

11)  9^4x / 27^3x = ?

(a) 9^x  (b) 1/3^x  (c) 1/9x  (d) 3^x  (e)  1/4^x

Solution

12) Which of the following is equal to 5^8x?

I. (5^4x)⁴

II. (5^4x)²

III. (5^4x)(5^4x)

(a) I  (b) II    (c) III  (d)  I and II    (e)  II and III

Solution

13)  n³ ≥ n² for which of the following?

I. n = 1

II. n = 0

III. n = −1

A. I   B. II   C. III   D. I and II   E. II and III

Solution

14)  Simplify (a²b^-6c¹¹d^-4) / (a^-5b^-2c⁷d⁹)           Solution

15)  27^4/x = 81, x = ?        Solution

16)  3√x-7 = 5, x = ?                Solution

17)  9√x - 7√x - 36 = -16, x = ?

(a) 5   (b) 10   (c) 20   (d) 50  (e) 100

Solution

18)  x = 2, y = x², (y²-x³)(x²/3y) = 

Solution