MISSING ANGLES IN PARALLELOGRAMS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Find the measures of the indicated angles in each parallelogram.
Problem 1 :
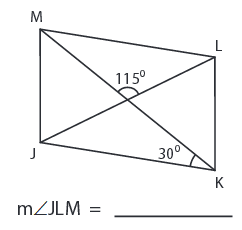
Problem 2 :
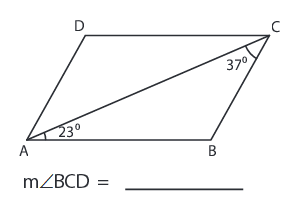
Problem 3 :
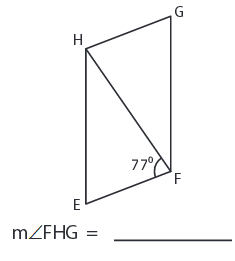
Problem 4 :
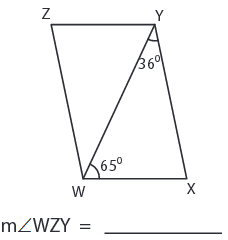
Problem 5 :
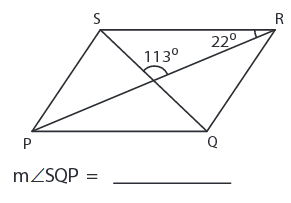
Problem 6 :
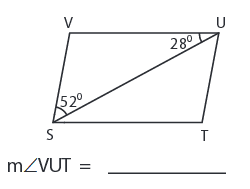
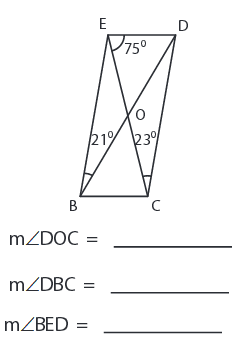
Problem 6 :
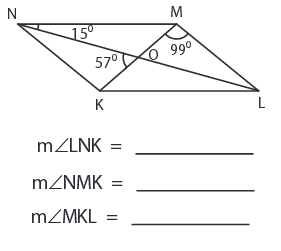
Problem 7 :
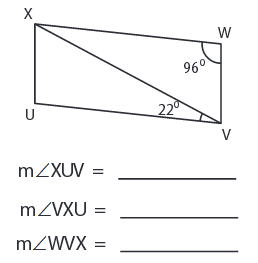
Problem 8 :
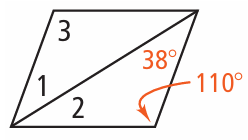
Find the measures of the numbered angles for each parallelogram.
Problem 9 :
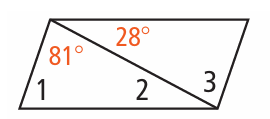
Problem 10 :
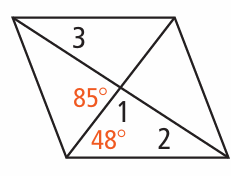
Problem 11 :
Problem 12 :
ABCD is a parallelogram in which ∠DAB = 70o and ∠CBD = 55o. Find ∠CDB and ∠ADB.
Problem 13 :
In a parallelogram ABCD, ∠A = (2x + 10)o and ∠C = (3x – 20)o. Find the value of x.
Problem 14 :
The sum of the two opposite angles of a parallelogram is 150o. Find all the angles of the parallelogram.
Problem 15 :
If the angles of a quadrilateral are (x – 20)o, (x + 20)o, (x – 15)o and (x + 15)o, find x and the angles of the quadrilateral
Answer Key
1) ∠JLM = 35°
2) ∠BCD = 60°
3) ∠FHG = 77°
4) ∠WZY = 79°
5) ∠SQP = 45°
6) ∠VUT = 80°
7) ∠LNK = 24°, ∠OMN = 42°, ∠NMK = 42°
8) ∠XUV = 96°, ∠VXU = 62°, ∠WVX = 62°
9) ∠DOC = 136°, ∠DBC = 61°, ∠BED = 98°
10) ∠1 = 71, ∠2 = 28, ∠3 = 81
11) ∠1 = 95, ∠2 = 37, ∠3 = 37
12) ∠ADB = 55
13) x = 30
14) all four angles are 75, 75, 105 and 105.
15) the all four angles are 70, 110, 65 and 105.
Find the value of x that will make the shape a parallelogram and give a reason to support your answer.
Problem 1 :
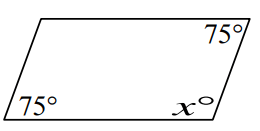
Problem 2 :
Solve for x in the parallelogram given below.
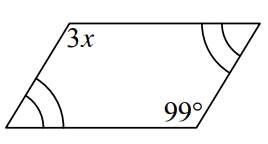
Problem 3 :
Solve for x in the parallelogram given below.
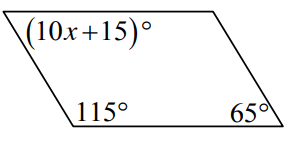
Problem 4 :
Solve for x and y in the parallelogram given below.
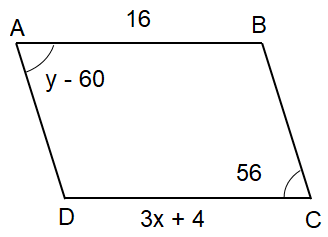
Problem 5 :
Use the diagram of parallelogram ABCD below to answer the questions.
|
1) Find CD 2) Find m∠ADB 3) Find m ∠BDC |
4) Find AC 5) Find m∠DCB 6) Find BE |
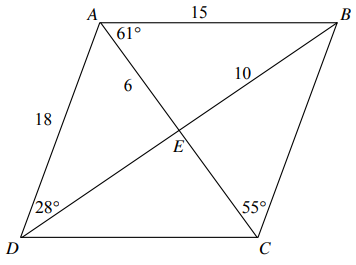
Problem 6 :
Solve for x and y in the parallelogram given below.
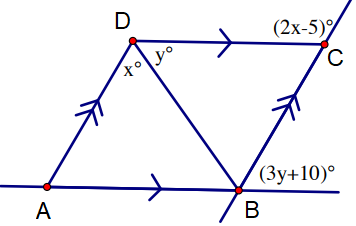
Problem 7 :
Find the missing value in each of the following parallelogram.
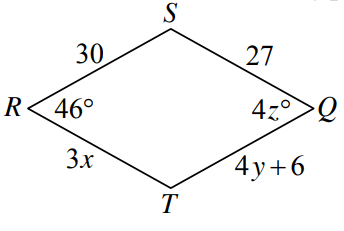
Problem 8 :
Given that quadrilateral ABCD is a parallelogram find the values of x and y.
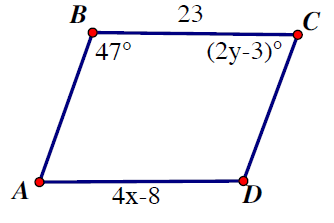
Problem 9 :
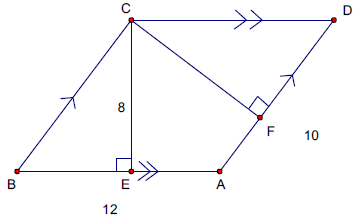
Find the length of CF. AB = 12, AD = 10, CE = 8.
Problem 10 :
Find the value of x that will make the shape a parallelogram and give a reason to support your answer.
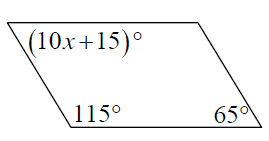
Find the value(s) of the variable(s) in each parallelogram
Problem 11 :
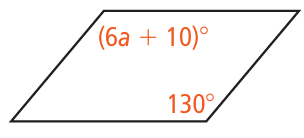
Problem 12 :
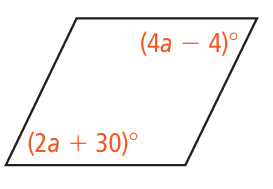
Problem 13 :
What are the values of x and y in the parallelogram?
- How are the angles related?
- Which variable should you solve for first?
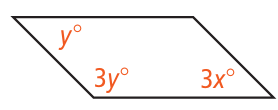
Problem 14 :
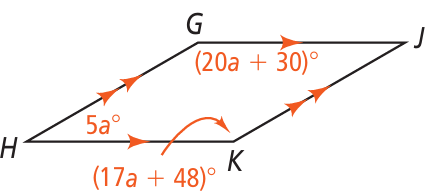
Problem 15 :
Two consecutive angles in a parallelogram have measures x + 5 and 4x - 10. Find the measure of the smaller angle.
Answer Key
1) x = 105
2) x = 33
3) x = 5
4) x = 4 and y = 116
5) (1) CD = 15 (2) ∠ADB = 28 (3) ∠BDC = 36
(4) BC = 12 (5) ∠DCB = 116 (6) BE = 10
6) x = 38 and y = 33
7) x = 9, y = 6 and z = 11.5
8) x = 31/4 and y = 68
9) CF = 9.6
10) x = 5
11) a = 20
12) a = 17
13) x = 15 and y = 45
14) a = 6
15) x = 37
Problem 1 :
From the parallelogram given below, find the value of x, y and z.
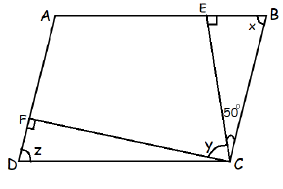
Problem 2 :
If one angle of a parallelogram is 24 degree less than twice the smallest angle then, find the largest angle of the parallelogram.
Problem 3 :
In a parallelogram PQRS, if
∠P = (3x − 5)° and ∠Q = (2x + 15)°
then find the value of x.
Problem 4 :
If PQRS is a parallelogram, then ∠P − ∠R is
(a) 90° (b) 45° (c) 60° (d) 0°
Problem 5 :
Two adjacent angles of a parallelogram are 3x - 4 and 3x + 10. Find the angles of parallelogram.
Problem 6 :
One angle of a parallelogram is 60 degree. Find its opposite angle and the adjacent angle.
Problem 7 :
Find the indicated measure in parallelogram MNOP, explain your reasoning.
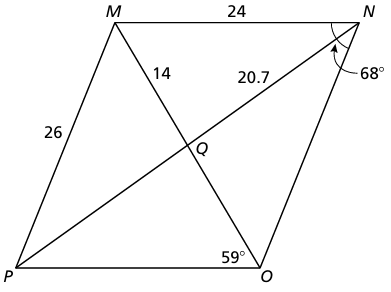
|
a) PO b) QO c) NO d) PQ |
e) m∠PMN f) m∠NOP g) m∠OPM h) m∠NMO |
Find the value of each of the variable in the parallelogram.
Problem 8 :
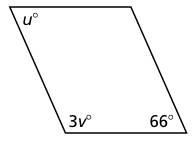
Problem 9 :
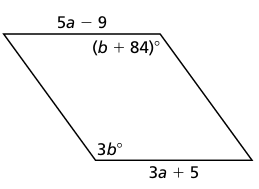
Problem 10 :
Find the value(s) of the variable(s) in each parallelogram
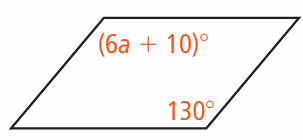
Problem 11 :
Two consecutive angles in a parallelogram have measures x + 5 and 4x - 10. Find the measure of the smaller angle.
Answer Key
1) x = z = 40 and y = 40
2) largest angle measure = 112.
3) x = 34
4) ∠P − ∠R = 0
5) angles are 83 and 97.
6) Adjacent angle = 120, opposite angle = 60
7) a) PO = 24 units
b) OQ = 14 units
c) NO = 26 units
d) PQ = 20.7 units
e) m∠PMN = 112
f) m∠NOM = 53
g) m∠OPM = 68
h) m∠NMO = 59
8) u = 66, v = 38
9) a = 7, b = 41
10) a = 20
11) smaller angle measure is 32 degree.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling