FINDING UNKNOWN ANGLES IN RHOMBUS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Find the all numbered angles in the following rhombus.
Problem 1 :
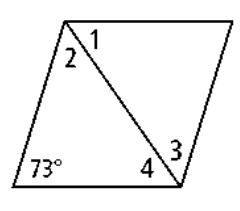
Problem 2 :
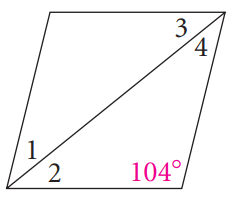
Problem 3 :
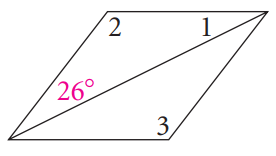
Problem 4 :
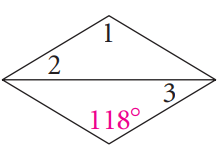
Problem 5 :
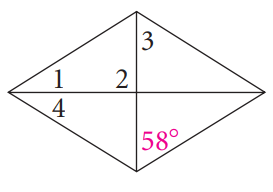
Problem 6 :
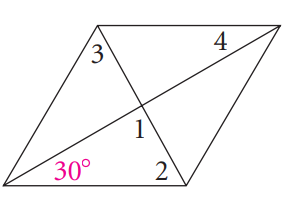
Problem 7 :
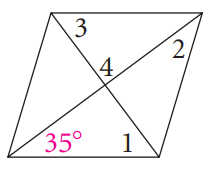
Problem 8 :
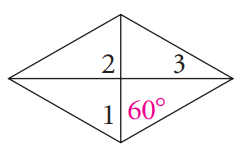
Problem 9 :
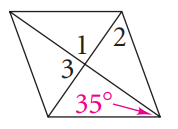
Problem 10 :
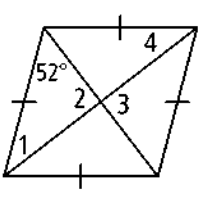
Problem 11 :
for any rhombus JKLM, decide whether the statement is always or sometimes true. Draw a diagram and explain your reasoning.
a) ∠L ≅ ∠M
b)∠K ≅ ∠M
c) JM ≅ KL
d) JK ≅ KL
e) JL ≅ KM
f) ∠JKM ≅ ∠LKM
Problem 12 :
Name each quadrilateral parallelogram, rectangle, rhombus, or square for which the statement is always true.
a) It is equiangular.
b) It is equiangular and equilateral.
c) The diagonals are perpendicular.
d) Opposite sides are congruent.
e) The diagonals bisect each other.
f) The diagonals bisect opposite angles.
Problem 13 :
Given a quadrilateral ABCD, and diagonals AC and BD bisect each other at P such that AP = CP and BP = DP. Also ∠APD = 90°, then quadrilateral is a
(a) rhombus (b) trapezium (c) parallelogram (d) rectangle
Answer Key
1) ∠1 = 53.5, ∠2 = 53.5, ∠3 = 53.5, ∠4 = 53.5
2) ∠1 = 38, ∠2 = 38, ∠3 = 38, ∠4 = 38
3) ∠1 = 26, ∠2 = 128, ∠3 = 128
4) ∠1 = 118, ∠2 = 31, ∠3 = 31
5) ∠1 = 32, ∠2 = 90, ∠3 = 58, ∠4 = 32
6) ∠1 = 90, ∠2 = 60, ∠3 = 60, ∠4 = 30
7) ∠1 = 55, ∠2 = 35, ∠3 = 55, ∠4 = 90
8) ∠1 = 60, ∠2 = 90, ∠3 = 30
9) ∠1 = ∠3 = 90, ∠2 = 55
10) ∠1 = 38, ∠2 = 90, ∠3 = ∠4 = 90
11)
a) In the rhombus JKLM, ∠L and ∠M are co-interior angles they add upto 180 degree. They are not congruent to each other. So, it is sometimes true.
b)∠K and ∠M are opposite angles and they are congruent. So, it is always true.
c) JM and KL are opposite sides, they must be equal. So, it is true always.
d) In rhombus all four sides will be equal then JK and KL are adjacent sides and they are equal. So, it is true always.
e) JL and KM are diagonals, so they are not equal always. Then it is sometimes true.
f) ∠JKM ≅ ∠LKM
The diagonals are angle bisector, then they must be equal. True always.
12)
a) In square, rectangle all angles measures must be 90 degree.
b) It is equiangular and equilateral.
All four angle measures will be equal and all side lengths will be equal in the shape of square.
c) The diagonals are perpendicular.
Diagonals are perpendicular in the shape of rhombus.
d) Opposite sides are congruent.
Opposite sides will be equal in the shapes parallelogram, square, rectangle and rhombus.
e) The diagonals bisect each other.
Diagonals will bisect each other in all the shapes parallelogram, square, rectangle and rhombus.
f) The diagonals bisect opposite angles.
In the quadrilaterals like parallelogram, square, rectangle and rhombus, the diagonals will bisect opposite angles.
13) Rhombus
Problem 1 :
For rhombus JMLK, find each angle measure.
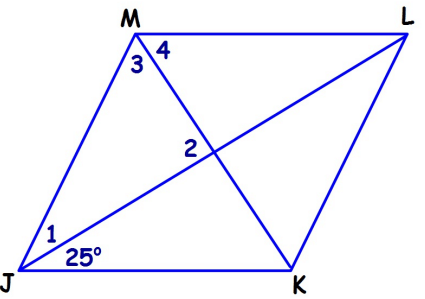
1) ∠1 2) ∠2 3) ∠3 4) ∠4 5) ∠JML 6) ∠MLK+
Problem 2 :
For rhombus JLMK, find each line segment and angle measure.
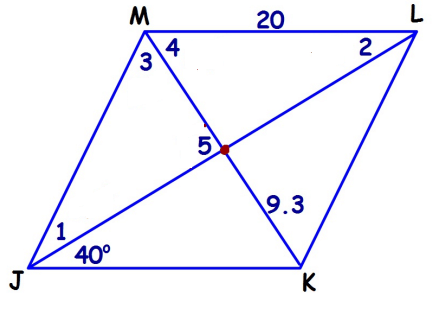
1) ∠1 2) ∠2 3) ∠3 4) ∠4 5) ∠5 6) LK 7) MK
Problem 3 :
For rhombus SLTM, find the missing values. If ∠1 = 3x + 8, ∠2 = 11x - 24, find
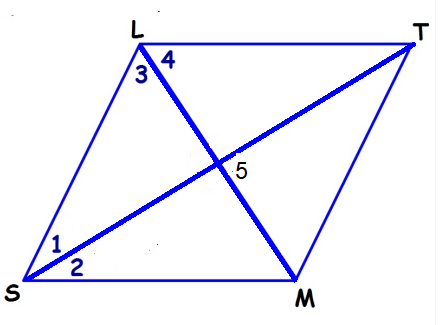
1) x = 2) ∠1 3) ∠2 4) ∠3 5) ∠4 6) ∠5
Problem 4 :
For rhombus SLTM, find the missing values, if ∠1 = 5x and ∠2 = x2 - 50, find
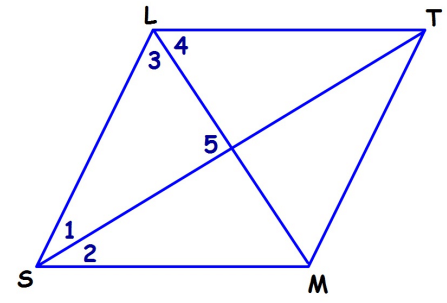
1) x = 2) ∠1 3) ∠2 4) ∠3 5) ∠4 6) ∠5
Problem 5 :
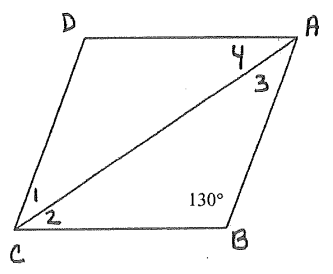
Find
1) ∠D 2) ∠DCB 3) ∠1 4) ∠2 5) ∠3 6) ∠4
Problem 6 :
Find all missing angles.
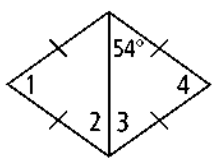
Problem 7 :
Find the measure of the numbered angles.
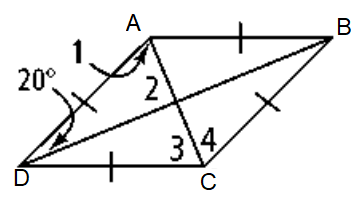
Using the properties of rhombuses, write and solve algebraic equation for each figure :
Problem 8 :
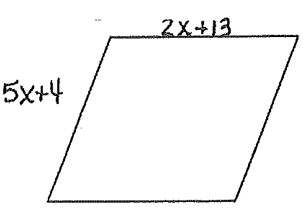
Problem 9 :
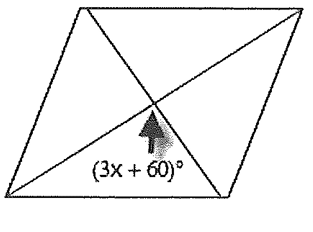
Problem 10 :
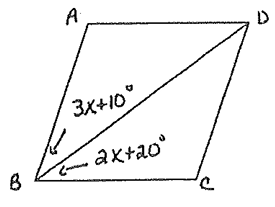
Problem 11 :
Answer Key
1) ∠1 = 25, ∠2 = 90, ∠3 = 65, ∠4 = 65, ∠JML = 130, ∠MLK = 50
2) ∠1 = 40, ∠2 = 40, ∠3 = 50, ∠4 = 50, ∠5 = 90, LK = 20, MK = 18.6
3) x = 4, ∠1 = 20, ∠2 = 20, ∠3 = 70, ∠4 = 70, ∠5 = 90
4) x = 10 and x = -5, ∠1 = 50, ∠2 = 50, ∠3 = 40, ∠4 = 40, ∠5 = 90
5) ∠D = 130, ∠DCB = 50, ∠1 = ∠2 = ∠3 = ∠4 = 25
6) ∠1 = 72, ∠2 = 54,∠3 = 54, ∠4 = 72
7) ∠1 = 70, ∠2 = 90, ∠3 = 70, ∠4 = 70
8) x = 3
9) x = 10
10) x = 10
11) x = 5
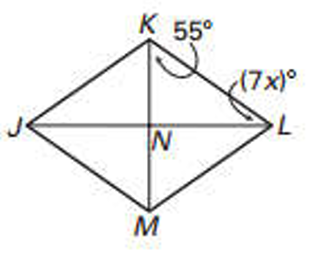
Find the value of x in each rhombus.
Problem 1 :
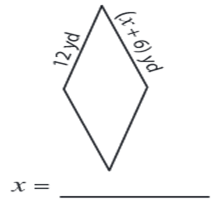
Problem 2 :
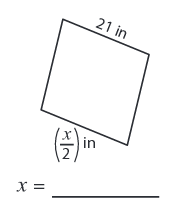
Problem 3 :
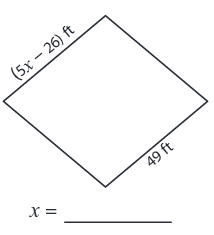
Problem 4 :
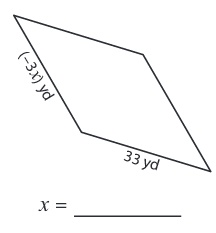
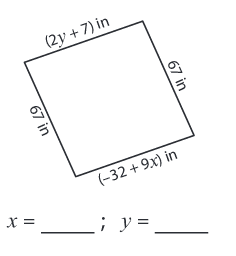
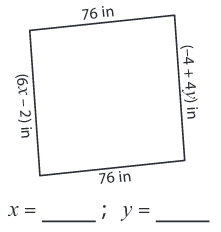
Find the value of x and y in each rhombus.
Problem 5 :
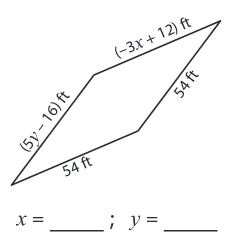
Problem 6 :
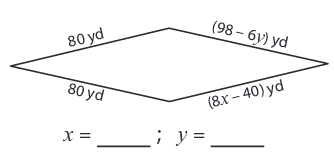
Problem 7 :
Problem 8 :
Problem 9 :
The diagonals of a rhombus are 6 cm and 8 cm respectively. Find the length of the sides of the rhombus. Also find its perimeter.
Problem 10 :
In rhombus PINK, PI = 3x + 7 and IN = x + 19, what is the value of NK?
Problem 11 :
The area of the rhombus shaped field is 5544 m2 and length of one diagonal is 72 m, what will be the perimeter of the field
a) 380 m b) 300 m c) 340 m d) 320 m
Answer Key
1) x = 6
2) x = 42
3) x = 15
4) x = -11
5) x = 11 and y = 30.
6) x = -14 and y = 14.
7) x = 15 and y = 3.
8) x = 13 and y = 20
9) Perimeter of rhombus = 20 cm
10) NK = 25
11) 340 m.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling