SOLVE FOR UNKNOWN IN RHOMBUS INVOLVING SIDE LENGTH

 Find the value of x in each rhombus.

Problem 1 :

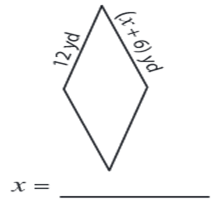
Solution :

Side length = 12 yd and (x + 6) yd

We know that all the sides are equal in a rhombus.

x + 6 = 12

x = 12 - 6

x = 6

Problem 2 :

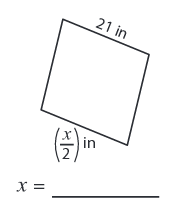
Solution :

Given, side length = 21 in and (x/2) in

We know that all the sides are equal in a rhombus.

x/2 = 21

x = 21 × 2

x = 42

Problem 3 :

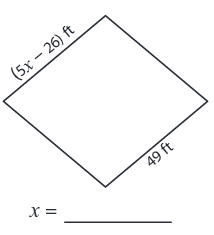
Solution :

Side length are 49 ft and (5x - 26) ft

We know that all the sides are equal in a rhombus.

5x - 26 = 49

5x = 49 + 26

5x = 75

x = 15

Problem 4 :

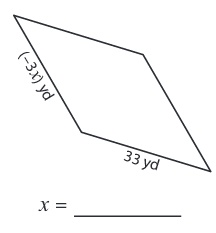
Solution :

Side length = 33 yd and (-3x) yd

We know that all the sides are equal in a rhombus.

-3x = 33

x = -33/3

x = -11

Find the value of x and y in each rhombus.

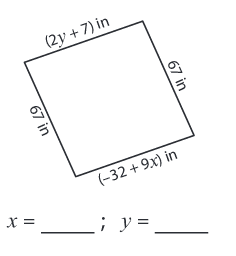
Problem 5 :

Solution :

Given, side length = (2y + 7) in, 67 in, (-32 + 9x) in and 67 in

We know that all the sides are equal in a rhombus.

So, x = 11 and y = 30.

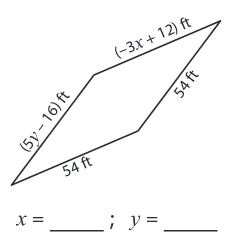
Problem 6 :

Solution :

Side lengths are (5y - 16) ft, 54 ft, (-3x + 12) ft and 54 ft

We know that all the sides are equal in a rhombus.

So, x = -14 and y = 14.

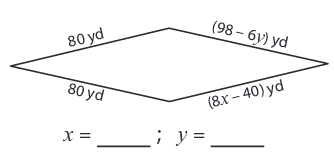
Problem 7 :

Solution :

Side lengths are (98 - 6y) yd, 80 yd, (8x - 40) yd and 80 yd

We know that all the sides are equal in a rhombus.

So, x = 15 and y = 3.

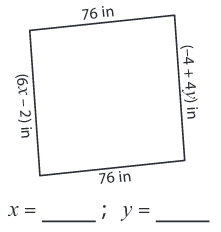
Problem 8 :

Solution :

Side lengths are (6x - 2) in, 76 in, (-4 + 4y) in and 76 in

We know that all the sides are equal in a rhombus.

So, x = 13 and y = 20.

Problem 9 :

The diagonals of a rhombus are 6 cm and 8 cm respectively. Find the length of the sides of the rhombus. Also find its perimeter.

Solution :

In rhombus the diagonals bisect each other and they are perpendicular.

Angle between two diagonals is 90 degree.

Let diagonals be d₁ and d₂

d₁ = 6 cm and d₂ = 8 cm

d₁/2 = 3 cm and d₂/2 = 4 cm

(Side)² = (d₁/2)² + (d₂/2)²

= 3² + 4²

= 9 + 16

(Side)² = 25

side = √25

= 5 cm

So, the side length of the square is 5 cm.

Perimeter of rhombus = 4(side length)

= 4(5)

= 20 cm

Problem 10 :

In rhombus PINK, PI = 3x + 7 and IN = x + 19, what is the value of NK?

Solution :

In the rhombus PINK, PI and IN are adjacent sides, they are equal. 

PI = NK

3x + 7 = x + 19

3x - x = 19 - 7

2x = 12

x = 12/2

x = 6

NK = x + 19

= 6 + 19

= 25

So, the side length of rhombus is 25 units.

Problem 11 :

The area of the rhombus shaped field is 5544 m² and length of one diagonal is 72 m, what will be the perimeter of the field 

a)  380 m   b)  300 m   c)  340 m   d)  320 m

Solution :

Area of rhombus = 5544 m²

Area of rhombus = (1/2) • d₁ • d₂ 

d₁ = 72 m

(1/2) • 72 •  d₂ = 5544

36d₂ = 5544

d₂ = 5544/36

d₂ = 154 m

d₁ = 72 m and d₂ = 154 m

d₁/2 = 36 m and d₂/2 = 77 m

(Side)² = (d₁/2)² + (d₁/2)²

= 36² + 77²

= 1296 + 5929

(Side)² = 7225

side = √7225

= 85 m

Side length of rhombus is 85 m, the perimeter of rhombus

= 4(85)

= 340 m

So, the perimeter of the field is 340 m. Option c is correct.