FINDING PERIMETER AND AREA OF SIMILAR FIGURES WORKSHEET

Problem 1 :

Triangle HIJ is similar to triangle STR, what is the perimeter of triangle STR

Solution

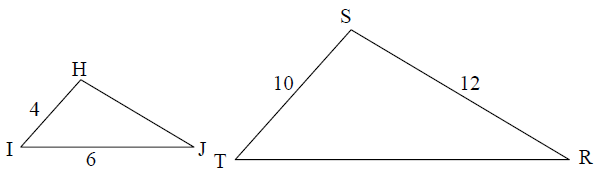
Problem 2 :

If the two triangles are similar

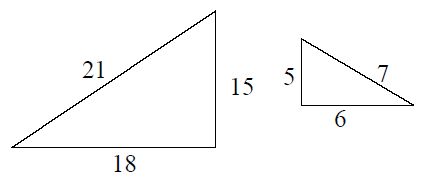
Find

i) Scale factor

ii) Ratio of perimeter

iii)  Ratio of area

Solution

Problem 3 :

Two triangles have a scale factor of 2/3. The area of the larger triangle is 12 cm². What is the area of smaller triangle.

Solution

Problem 4 :

If the length of each side of triangle is cut to 1/3 of its original size, what happens to the area of the triangle ?

The new area is _______________ of the original area.

Solution

Problem 5 :

For the two triangles below to be similar, which of the following be true ?

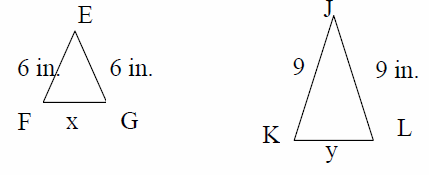
a)  x = 2y/3    b)  c = 3y/2     c)  x = 3y     d)  x = y

Solution

Problem 6 :

An architect is building a model of a tennis court for a new client. On the model, the court is 6 inches wide and 13 inches long. An official tennis court is 36 feet wide. What is the length of a tennis court ?

Solution

Problem 7 :

Your family has decided to put a rectangular patio in your backyard, similar to the shape of your backyard. Your backyard has a length of 45 feet and a width of 20 feet. The length of your new patio is 18 feet. Find the perimeters of your backyard and of the patio.

Solution

Problem 8 :

Rectangle A is similar to rectangle B. Rectangle A has side lengths of 6 and 12. Rectangle B has a side length of 18. What are the possible values for the length of the other side of rectangle B? Select all that apply.

a) 6       b) 9    c) 24     d) 36

Solution

Problem 9 :

What is the perimeter of the rectangle?

b) What is the area of the rectangle?

c) If the width of the rectangle is doubled, what do you think happens to the perimeter?

d) If the width of the rectangle is doubled, what do you think happens to the area?

Solution

The figures in each pair are similar. Compare the first figure to the second. Give the ratio of the perimeters and the ratio of the areas.

Problem 1 :

Solution

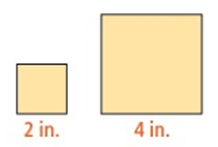
Problem 2 :

Solution

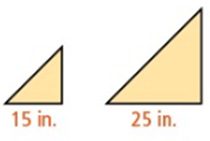
Problem 3 :

Solution

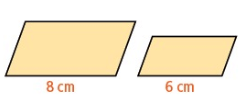
Find the scale factor and the ratio of perimeters for each pair of similar figures.

Problem 4 :

Two regular octagons with areas 4 ft² and 16 ft²

Solution

Problem 5 :

Two trapezoids with areas 49 cm² and 9 cm²

Solution

Problem 6 :

Two equilateral triangles with areas 16√3 ft² and √3 ft²

Solution

Problem 7 :

Two circles with areas 2π cm² and 200π cm²

Solution

Problem 8 :

Figure A has a perimeter of 60 inches and one of the side lengths is 5 inches. Figure B has a perimeter of 84 inches. Find the corresponding missing side length

Solution

Problem 9 :

Figure A has an area of 4928 square feet and one of the side lengths is 88 feet. Figure B has an area of 77 square feet. Find the corresponding missing side length.

Solution

Problem 10 :

a) For the pair of similar triangles below, list the corresponding angles and the corresponding sides.

b) Determine all unknown side lengths to the nearest tenth of a unit and determine all unknown angles

Solution

The scale factor between two similar figures is given. The surface area and volume of the smaller figure are given. Find the surface area and volume of the larger figure.

Problem 1 :

Scale factor = 1 : 2

SA = 90 yd²

V = 216 yd³

Solution

Problem 2 :

Scale factor = 4 : 9

SA = 256 km²

V = 1536 km³

Solution

Problem 3 :

The dimensions of the touch tank at an aquarium are doubled. What is the volume of the new touch tank?

A) 150 ft³       B) 4000 ft³    C) 8000 ft³    D) 16,000 ft³ 

The solids are similar. Find the volume of the red solid. Round your answer to the nearest tenth.

Solution

Problem 4 :

Solution

Problem 5 :

Solution

Problem 6 :

A and B are mathematically similar.

The height of A : the height of B = 3 : 5

(a) Find the surface area of A : the surface area of B

(b) Find the volume of A : the volume of B

Solution

Problem 7 :

Two solid toys, C and D, are similar.

The volume of toy C is 40 cm³

The surface area of C : surface area of D = 2 : 9

Work out the volume of toy D.

Solution

Problem 8 :

Washing powder is sold in two different sizes, a large box A and a smaller box B. Cuboid boxes A and B are similar.

Surface area of A : Surface area of B = 81 : 4

How many smaller boxes, B, can be completely filled using the contents of a full box A?

Solution

Problem 9 :

The volumes of two similar shapes are in the ratio 1000 : 27

The surface area of the larger shape is 250 cm² Work out the surface area of the smaller shape

Solution

Problem 10 :

Shown are similar solids G and H.

The volume of G : the volume of H = 27 : 1000

(a) Find the height of G : the height of H

(b) Find the surface area of G : the surface area

Solution