FINDING SCALE FACTOR OF SIMILAR FIGURES AND FIND PERIMETER

If the sides of a rectangle are multiplied by k, a similar rectangle is obtained.

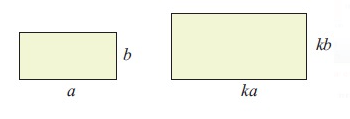
Finding the perimeter :

Perimeter of old shape = 2 (a + b)

Perimeter of new shape = 2(ka + kb)

= 2k(a + b)

Note :

If two shapes are similar, then their perimeter are proportional to the measures of the corresponding sides.

More simply, if two shapes are in the ratio a : b, then its perimeter will also be in the ratio a : b.

If two shapes are in the ratio a : b, then its area will be in the ratio a² : b². 

The figures in each pair are similar. Compare the first figure to the second. Give the ratio of the perimeters and the ratio of the areas.

Problem 1 :

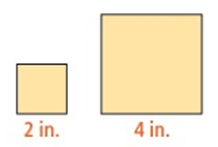
Solution :

Ratio of corresponding sides = 2 : 4

Ratio of perimeter = a : b

= 2 : 4

a : b = 1 : 2

Ratio of area = a² : b²

= 1² : 2²

a² : b² = 1 : 4

Problem 2 :

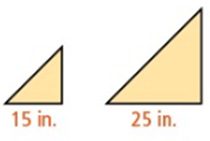
Solution :

Ratio of corresponding sides = 15 : 25

Ratio of perimeter = a : b

= 15 : 25

a : b = 3 : 5

Ratio of area = a² : b²

= 3² : 5²

a² : b² = 9 : 25

Problem 3 :

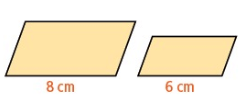
Solution :

Ratio of corresponding sides = 8 : 6

Ratio of perimeter = a : b

= 8 : 6

a : b = 4 : 3

Ratio of area = a² : b²

= 4² : 3²

a² : b² = 16 : 9

Find the scale factor and the ratio of perimeters for each pair of similar figures.

Problem 4 :

Two regular octagons with areas 4 ft² and 16 ft²

Solution :

a² : b² = 4 : 16

a : b = √4 : √16

a : b = 2 : 4

a : b = 1 : 2

Problem 5 :

Two trapezoids with areas 49 cm² and 9 cm²

Solution :

a² : b² = 49 : 9

a : b = √49 : √9

a : b = 7 : 3

Problem 6 :

Two equilateral triangles with areas 16√3 ft² and √3 ft²

Solution :

a²: b² = 16√3: √3

a: b = 4: 1

Problem 7 :

Two circles with areas 2π cm² and 200π cm²

Solution :

a² : b² = 2π : 200π

a : b = 1 : 100