FIND THE DIAGONAL OF 3D SHAPES WORKSHEET

Problem 1 :

Find the length of the diagonal D of the following rectangular prism.

Solution

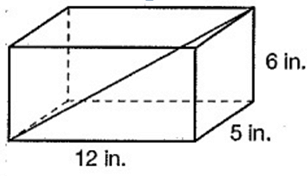
Problem 2 :

Find the length of the diagonal D of the following rectangular prism.

Solution

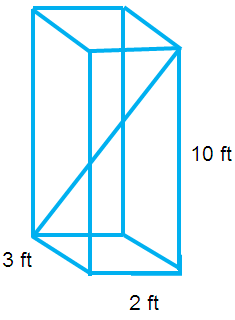
Problem 3 :

Find the length of the diagonal D of the following rectangular prism.

Solution

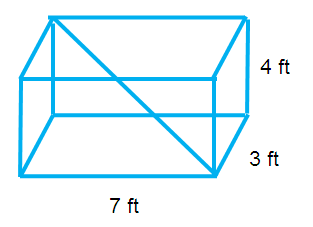
Problem 4 :

Find the length of the diagonal D of the following rectangular prism.

Solution

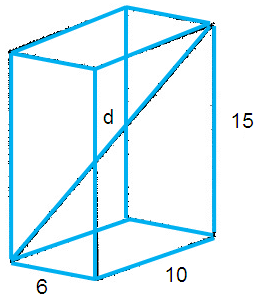
Problem 5 :

what is the longest object that Simone can put in a rectangular box that is 10 inches wide, 12 inches long and 20 inches tall? round to the nearest tenth of an inch.

Solution

Problem 6 :

A rectangular prism is 12 inches wide, 5 inches long and 6 inches tall. Tamara’s work to find the length of its longest diagonal is to the right. Unfortunately, she made a mistake. Identify the mistake and find the length of the longest diagonal in the rectangular prism

Solution

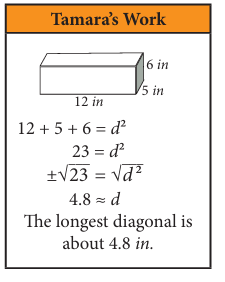
Problem 7 :

A rectangular prism is 3 feet long, 4 feet wide and 2 feet tall. What is the length of its longest diagonal?

Solution

Problem 8 :

Petra is sending her brother a giant candy cane stick for a gift. She will use a box that measures 10 inches by 6 inches by 2 inches. What is the maximum length the candy cane stick can be to fit in the box?

Solution

Problem 9 :

Elena needs to ship a 61 cm concert flute to a customer. She has two rectangular boxes. One is 25 cm by 25 cm by 50 cm. The other box is 10 cm by 12 cm by 58 cm.

a. What is the longest object that will fit in the 25 cm × 25 cm × 50 cm rectangular box?

b. What is the longest object that will fit in the 10 cm × 12 cm × 58 cm rectangular box?

c. In which box will the flute best fit?

Solution

Problem 10 :

A cube has a surface area of 600 square meters.

a. How many faces does a cube have?

b. What is the area of one face of the cube?

c. Find the length of one edge of the cube.

d. What is the length of the cube’s longest diagonal? Use mathematics to justify your answer.

Solution

Problem 1 :

A cylindrical can of seltzer has a height of 5 inches and a radius of 1 inch, as shown.

Solution

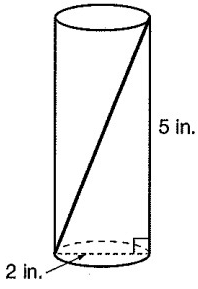
Problem 2 :

Find the length of the diagonal of shown below.

Solution

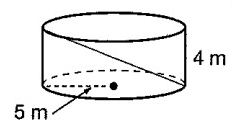
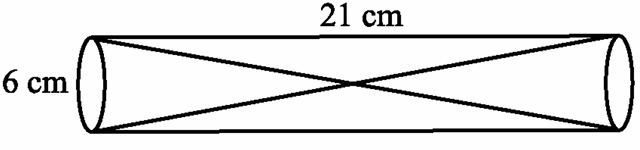
Problem 3 :

Find the length of the diagonal of shown below.

Solution

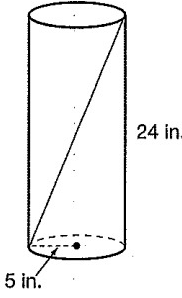
Problem 4 :

An oil tank is in the shape of a cylinder. A dipstick can be used to measure the amount of oil in the tank.

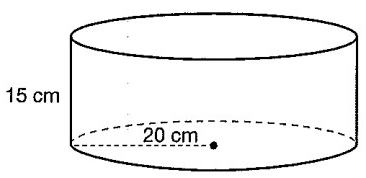
The dipstick has a length that is an integer value. What is the smallest possible length of a dipstick that cannot be submerged completely in the oil tank?

Solution

Problem 5 :

Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12√ 3 cm. Find the edges of the three cubes

Problem 6 :

Two solid cones A and B are placed in a cylindrical tube as shown in the below figure. The ratio of their capacities are 2 : 1. Find the heights and capacities of cones. Also find the volume of the remaining portion of the cylinder.

Problem 7 :

If the length of the diagonal of a cube is 6√3 m, find the volume of it.

Problem 8 :

The sum of length, width and height of a cuboid is 19 cm and its diagonal is 5√5 cm. What is its surface area?

Problem 1 :

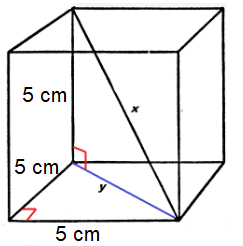
Find the value of x.

Solution

Problem 2 :

Find the lateral surface area of a cube, if its diagonal is √6 cm.

Solution

Problem 3 :

The side length of a cube is 5 meters. What is the length of its diagonal across one of the faces?

Solution

Problem 4 :

Find the length of the face diagonal of a cube when the side measures 9 units. Use the diagonal face formula of a cube.

Solution

Problem 5 :

The length of the diagonal of a cube that can be inscribed in a sphere of radius 7.5 cm is

Solution

Problem 6 :

Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12√3 cm. Find the edges of the three cubes

Solution

Problem 7 :

Find the length of the longest rod that can be placed in a room 12 m long, 9 m broad and 8 m high.

Solution

Problem 8 :

Find the length of the longest pole that can be placed in a room 12 m long 3 m wide and 9 m high.

Solution

Problem 9 :

If the length of a diagonal of a cube is 7√3 cm each of its side is

a)  7 cm    b) 49 cm     c) 343 cm    d)  14 cm

Solution

Problem 10 :

The length of a diagonal of a cube whose side measures 3 cm is ______________ 

Solution

Problem 11 :

The length of an edge of a hollow cube open at one face is √3 meter. what is the length of the largest pole that it can accommodate?

Solution

Problem 12 :

The surface area pf cube is 600 cm². Find the length of its diagonal.

Solution

Answer Key

1) x = 5√3, y = 5√2

2)  8 cm²

3)  5√3

4) length of one face of diagonal = 9√2

5) 15√2

6)  the side lengths of cube is 6 cm, 8 cm and 10 cm respectively.

7)  17 m is the length of the longest rod that can be placed in the room.

8)  the longest pole that can be placed is 15.29 m.

9) a)  7 cm 

10) the required side length of the diagonal is 3√3 cm.

11) the longest pole can be fixed in the cube is 3 meters.

12)  10√3