FIND THE DIAGONAL OF A RECTANGULAR PRISM

Find the length of the diagonal of a rectangular prism :

The following picture shows, how to find the diagonal of a rectangular prism.

Problem 1 :

Find the length of the diagonal D of the following rectangular prism.

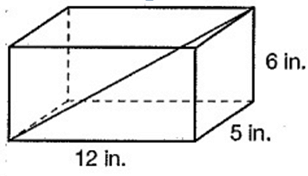
Solution :

Considering the base of the rectangular prism, it is in the shape of rectangle.

l = 12 in, w = 5 in

In the base, diagonal length is,

l² + w² = d²

12² + 5² = d²

144 + 25 = d²

169 = d²

13 = d

So, the diagonal length of the base is13 in.

Length of the diagonal of the rectangular prism be D.

6² + 13² = D²

36 + 169 = D²

205 = D²

√205 = D

So, the diagonal length of the prism is√205 in.

Problem 2 :

Find the length of the diagonal D of the following rectangular prism.

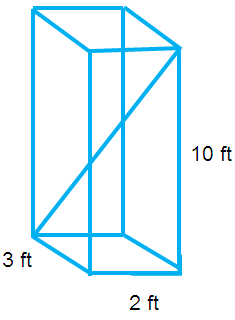
Solution :

Length = 3 ft, width = 2 ft and height = 10 ft

Diagonal = √3² + 2² + 10²

= √9+4+100

= √113 inches

Problem 3 :

Find the length of the diagonal D of the following rectangular prism.

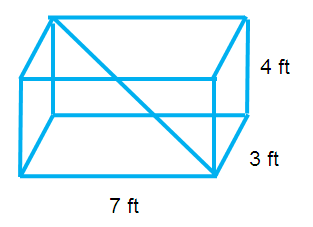
Solution :

Length = 7 ft, width = 3 ft and height = 4 ft

Diagonal = √7² + 3² + 4²

= √49 + 9 + 16

= √74 ft

Problem 4 :

Find the length of the diagonal D of the following rectangular prism.

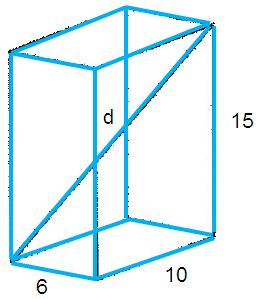
Solution :

Length = 10 ft, width = 6 ft and height = 15 ft

Diagonal = √10² + 6² + 15²

= √100 + 36 + 225

= √361

= 19 ft