HOW TO FIND DIAGONAL OF CYLINDER

Problem 1 :

A cylindrical can of seltzer has a height of 5 inches and a radius of 1 inch, as shown.

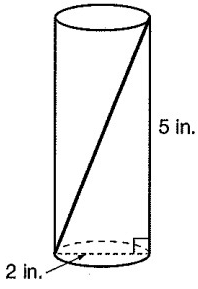
Solution :

h = 5 in, r = 2 in.

Diagonal of cylinder c² = a² + b²

c² = 5² + 2²

= 25 + 4

= 29

c = √29

So, diagonal of the cylinder √29in.

Problem 2 :

Find the length of the diagonal of shown below.

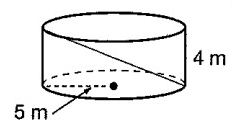
Solution :

h = 4 m and r = 5 m

Diagonal of cylinder c² = a² + b²

c² = 4² + (10)²

= 16 + 100

= 116

d = √116

d = 10.8

So, diagonal of the cylinder is 10.8.

Problem 3 :

Find the length of the diagonal of shown below.

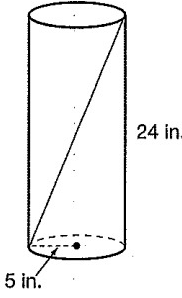
Solution :

By observing the figure,

Height h= 24 in.

Radius r = 5 in.

Diagonal of cylinder c² = a² + b²

d² = (10)² + (24)²

= 100 + 576

= 676

d = √676

d = 26

So, diagonal of the cylinder is 26.

Problem 4 :

An oil tank is in the shape of a cylinder. A dipstick can be used to measure the amount of oil in the tank.

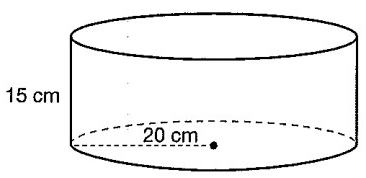
The dipstick has a length that is an integer value. What is the smallest possible length of a dipstick that cannot be submerged completely in the oil tank?

Solution :

Height h= 15 cm

Radius r = 20 cm

Diagonal of cylinder c² = a² + b²

c² = (40)² + (15)²

= 1600 + 225

= 1825

d = √1825

d = 42.72

diagonal of the cylinder is 42.72

So, length of dipstick 43 cm.

Problem 5 :

Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12√ 3 cm. Find the edges of the three cubes

Solution :

Let 3x, 4x and 5x are side lengths of each cube.

Volume of large cube = Volume of three small cubes

Let A be the side length of large cube.

A³ = (3x)³ + (4x)³+ (5x)³

= 27x³ + 64x³ + 125x³

A³ = 216x³

A = ∛216x³

A = 6x

Side length of large cube is 6x.

Length of diagonal of square face = √2a(when a is the side length)

= 6x√2

Given that, Diagonal of cube = 12√3

Diagonal of cube = Side length ⋅ (√3)

Side length of new cube = 12

216x³ = 12³

(6x)³ = 12³

6x = 12

x = 12/6

x = 2

3x ==> 3(2) ==> 6

4x ==> 4(2) ==> 8

5x ==> 5(2) ==> 10

So, side lengths of cube is 6 cm, 8 cm and 10 cm respectively.

Problem 6 :

Two solid cones A and B are placed in a cylindrical tube as shown in the below figure. The ratio of their capacities are 2 : 1. Find the heights and capacities of cones. Also find the volume of the remaining portion of the cylinder.

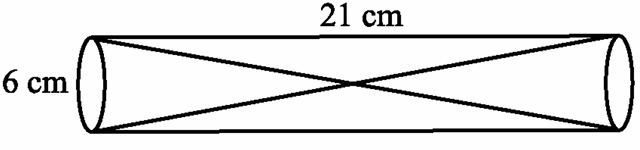
Solution :

From the figure,

Radius of cone A = 6/2 = 3 cm

Radius of cone B = 6/2 = 3 cm

Let the height of cone A be h₁

So, height of cone B = 21 - h₁

Volume of cone A = (1/3)π(3)²h₁

= 3πh₁ cm³

Volume of cone B = (1/3)π(3)²(21 - h₁)

= 3π(21 - h₁)

= 63π - 3πh₁ cm³

Given, volume of cone A : volume of cone B = 2:1

So, volume of cone A = 2 × volume of cone B ------------------ (1)

3πh₁ = 2(63π - 3πh₁)

 3πh₁ = 126π - 6πh₁

3πh₁ + 6πh₁ = 126π

9πh₁ = 126π

9h₁ = 126

h₁ = 126/9

h₁ = 42/3 cm

h₁ = 14 cm

Height of cone B = 21 - 14 = 7 cm

Volume of cone A = 3(22/7)(42/3)

= (22)(6)

= 132 cm³

From (1), Volume of cone B = volume of cone A/2

= 132/2

= 66 cm³

Volume of cylinder = πr²h

Given, r = 6/2 = 3 cm

h = 21 cm

Volume of cylinder = (22/7)(3)²(21)

= (22)(9)(3)

= 22(27)

= 594 cm³

Volume of the remaining portion = volume of cylinder - volume of cone A - volume of cone B

= 594 - 132 - 66

= 594 - 198

= 396 cm³

Therefore, the volume of the remaining portion is 396 cm³

Problem 7 :

If the length of the diagonal of a cube is 6√3 m, find the volume of it.

Solution :

Length of the diagonal of cube = 6√3

Length of diagonal = √3(side length)

Side length of cube = 6

volume of cube = 6³

= 216

So, volume of cube is 216 m³

Problem 8 :

The sum of length, width and height of a cuboid is 19 cm and its diagonal is 5√5 cm. What is its surface area?

Solution :

Sum of length, width and height = 19 cm

l + w + h = 19

Length of diagonal = 5√5 cm

Diagonal = √l² + w² + h²

(5√5)² = l² + w² + h²

25(5) = l² + w² + h²

 l² + w² + h² = 75

(l + w + h)² = l² + w² + h² + 2(lw + wl + hl)

19² = l² + w² + h² + 2(lw + wl + hl) ----(1)

Applying the value of  l² + w² + h² = 75 in (1), we get

361 = 75 + 2(lw + wl + hl)

361 - 75 = 2(lw + wl + hl)

286 = 2(lw + wl + hl)

Total surface area is 286 cm²

So, the required total surface area is 286 cm^2.