EEXAMPLES OF GRAPHING RATIONAL FUNCTIONS
To graph any rational function, we have to analyze the following.
Discontinuity of function :
A discontinuous function is a function in algebra that has a point where either the function is not defined at the point.
How to find discontinuity of the function ?
By equating the denominator to zero, we can find the point of discontinuity.
Hole of a function :
A hole exists on the graph of a rational function at any input value that causes both the numerator and denominator of the function to be equal to zero.
By equating the common factor to zero, we can find the hole.
Horizontal asymptotes :
A horizontal asymptote is a horizontal line that is not part of a graph of a function but guides it for x – values “far” to the right and/or “far” to the left.
Case 1 :
degree of numerator = degree of denominator
y = leading coefficient of N(x)/leading coefficient of D(x).
Case 2 :
degree of numerator < degree of denominator
y = 0 which is the x – axis.
Case 3 :
degree of numerator > degree of denominator
There is no horizontal asymptote.
Vertical Asymptotes :
The Vertical Asymptotes of a rational function are found using the zeros of the denominator.
X-intercept :
x-intercept of a rational function can be found by equation y = 0.
Domain :
The domain of a rational function is the set of all numbers except the zeros of the denominator.
Identify the points of discontinuity, holes, vertical asymptotes, x – intercepts, horizontal asymptote, and domain of each. Then sketch the graph.
Example 1 :
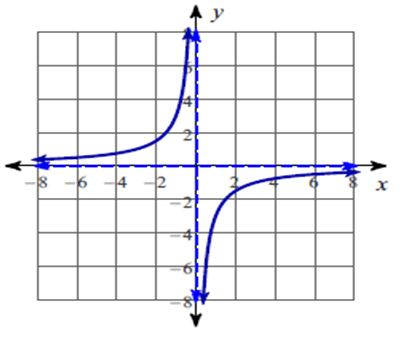
f(x) = -3/x
Solution :
Discontinuity :
f(x) = -3/x
The function is discontinuous at x = 0.
Holes :
None
Vertical asymptote :
f(x) = -3/x
So, the vertical asymptotes at x = 0.
X – intercepts :
f(x) = -3/x
So, the x – intercepts is none.
Horizontal asymptote :
f(x) = -3/x
degree of numerator < degree of denominator
So, equation of the horizontal asymptote is y = 0 which is the x – axis.
Domain :
When x = 0
So, all real values except 0.
Example 2 :
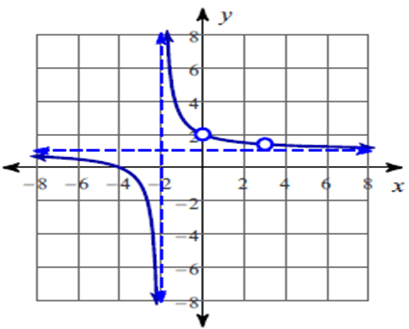
f(x) = (x3 + x2 – 12x)/(x3 – x2 – 6x)
Solution :
Discontinuity :
f(x) = (x3 + x2 – 12x)/(x3 – x2 – 6x)
x3 + x2 – 12x = x(x2 + x – 12)
x3 – x2 – 6x = x(x2 – x – 6)
By factoring,
x2 + x – 12 = (x - 3) (x + 4)
x2 – x – 6 = (x + 2) (x – 3)
f(x) = x(x – 3) (x + 4)/x(x + 2) (x – 3)
|
x = 0 |
x + 2 = 0 x = -2 |
x – 3 = 0 x = 3 |
The function
is discontinuous at x = 0, x = -2 and x = 3.
Holes :
x = 0
x – 3 = 0
x = 3
So, there is a hole at x = 0, x = 3.
Vertical asymptote :
x + 2 = 0
x = -2
So, the vertical asymptote at x = -2.
X – intercepts :
f(x) = x(x – 3) (x + 4)/x(x + 2) (x – 3)
X – intercepts occurs when y = 0.
f(0) = (x + 4)/(x + 2)
x + 4 = 0
x = -4
So, the x – intercepts is -4.
Horizontal asymptote :
f(x) = (x3 + x2 – 12x)/(x3 – x2 – 6x)
degree
of numerator = degree of denominator
y = leading coefficient of N(x)/leading coefficient of D(x).
So, equation of the horizontal asymptote is y = 1.
Domain :
When x = 0 ,x + 2 = 0 and x – 3 = 0
x = 0, x = -2 and x = 3
So, all real values except 0, -2 and 3.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling