HOW TO FIND THE POINT OF DISCONTINUITY OF A RATIONAL FUNCTION

Find any points of discontinuity for each rational function.

Problem 1 :

y = (x + 3)/(x – 4) (x + 3)

Solution :

To find points of discontinuity, let us equate the denominators to 0.

y = (x + 3)/(x – 4) (x + 3)

x – 4 = 0

x = 4

x + 3 = 0

x = -3

The function is discontinuous at x = -3 and 4.

Problem 2 :

y = (x - 2)/(x² – 4)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = (x - 2)/(x² – 4)

x² – 4 = 0

(x + 2)(x - 2) = 0

x + 2 = 0 and x - 2 = 0

x = -2 and x = 2

The function is discontinuous at x = ±2.

Problem 3 :

y = (x - 3) (x + 1)/(x – 2)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = (x - 3) (x + 1)/(x – 2)

x – 2 = 0

x = 2

The function is discontinuous at x = 2.

Problem 4 :

y = 3x(x + 2)/x(x + 2)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = 3x(x + 2)/x(x + 2)

x(x + 2) = 0

x = 0, x + 2 = 0

x = -2

The function is discontinuous at x = 0, -2.

Problem 5 :

y = 2/(x + 1)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = 2/(x + 1)

x + 1 = 0

x = -1

The function is discontinuous at x = -1.

Problem 6 :

y = 4x/(x³ – 9x)

Solution :

To find point of discontinuity, let us equate the denominator to 0.

y = 4x/(x³ – 9x)

x³ – 9x = 0

x(x² - 9) = 0

x(x² - 3²) = 0

x(x + 3)(x - 3) = 0

x = 0, x = 3 and x = -3

The function is discontinuous at x = 0, ±3.

Problem 7 :

Check the function

g(x) = (x² + 7x + 10)/(x - 3)(x + 2)

for discontinuities. Conduct appropriate tests to determine if asymptotes exist at the discontinuity values. State the equations of any asymptotes and the domain of g(x)

Solution :

g(x) = (x² + 7x + 10)/(x - 3)(x + 2)

Factoring the numerator, we get

= (x + 5)(x + 2)/(x - 3)(x + 2)

Since the common factor is (x + 2), there must be a hole at x = -2.

x - 3 = 0

x = 3

Domain is all real values except -2 and 3.

Problem 8 :

Match the equation of each rational function with the most appropriate graph. Explain your reasoning.

a) y = (x + 4) / (x² - 3x - 4)

b) y = (x + 4) / (x² + 5x + 4)

c) y = (x² + 4x)/(x + 4)

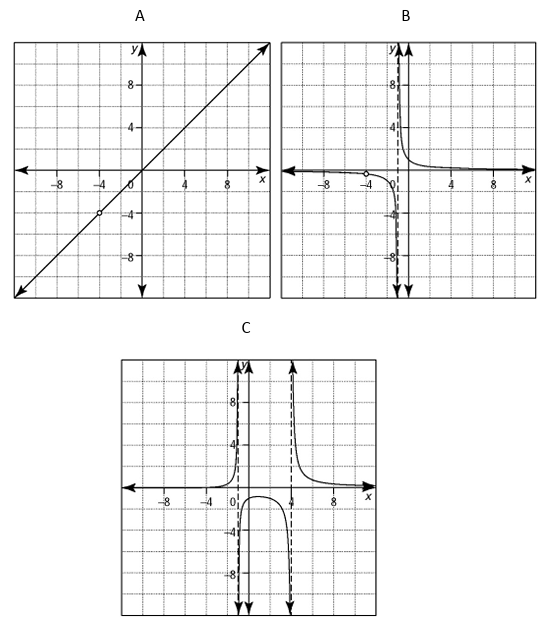
Solution :

a) y = (x + 4) / (x² - 3x - 4)

Factoring the denominator, we get

y = (x + 4) / (x - 4) (x + 1)

Since there is no common factor, there is no hole.

x - 4 = 0 and x + 1 = 0

x = 4 and x = -1

The function is discontinuous at x = 4 and x = -1. Vertical asymptotes are at x = 4 and x = -1. Option c matches these conditions.

b) y = (x + 4) / (x² + 5x + 4)

Factoring the denominator, we get

y = (x + 4) / (x + 4) (x + 1)

There is a hole at x = -4

x + 1 = 0

x = -1

The function is discontinuous at x = -1. Vertical asymptote is at x = -1. Option b matches these conditions.

c) y = (x² + 4x)/(x + 4)

Factoring the numerator, we get

y = x(x + 4)/(x + 4)

(x + 4) is a common factor, then there must be hole

x + 4 = 0

x = -4

There is hole at x = -4. There is no vertical asymptote. So, option a matches this condition.

Problem 9 :

Write the equation for each graphed rational function.

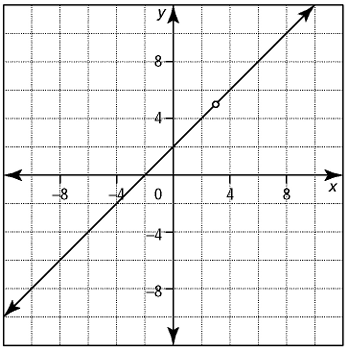
Solution :

By observing the figure, there is hole at x = 3, since it straight line and y-intercept is b = 2

Slope = 1

y = mx + b

y = x + 2

The common factor at the numerator and denominator is (x - 3)

y = (x + 2)(x - 3)/(x - 3)

Problem 10 :

Write the equation for each graphed rational function.

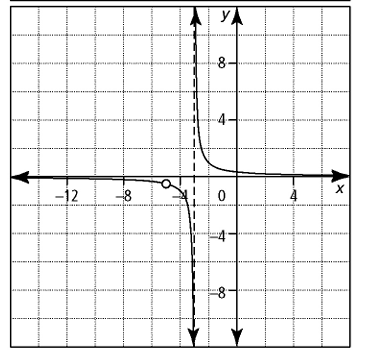
Solution :

By observing the figure, there is hole at x = -5

• The common factor at the numerator and denominator is (x + 5). The graph is the parent graph of reciprocal function (1/x). 
• Moving the graph 3 units towards the left, then the function will be x + 3

y = (x + 5)/(x + 5)(x + 3)