CO INETRIOR ANGLES PRACTICE WORKSHEET

Find the values of the variables in the following :

Problem 1 :

Solution

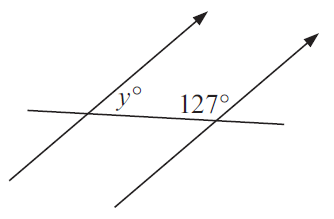
Problem 2 :

Solution

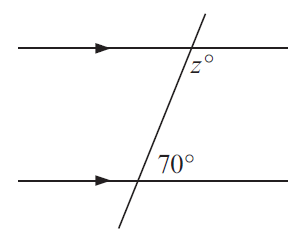
Problem 3 :

Solution

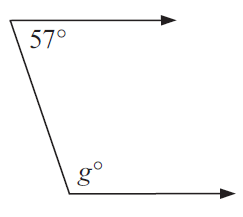
Problem 4 :

Solution

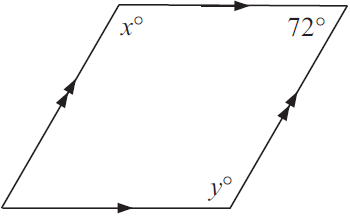
Problem 5 :

Solution

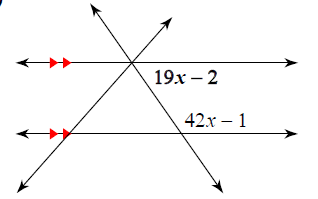
Problem 6 :

Solution

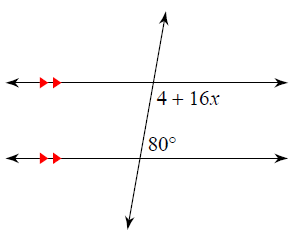
Problem 7 :

Solution

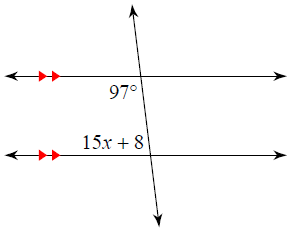
Problem 8 :

a) Name a pair of complementary angles, a pair of supplementary angles, and a pair of adjacent angles.

b) Are ∠KGH and ∠LKG adjacent angles? Are ∠FGK and ∠FGH adjacent angles? Explain.

c) ∠1 is a complement of ∠2, and m∠2 = 5°. Find m∠1.

d) ∠3 is a supplement of ∠4, and m∠3 = 148°. Find m∠4.

Solution

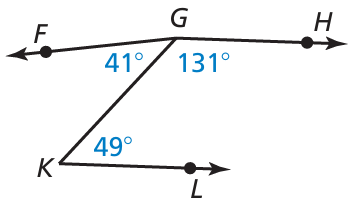
Problem 9 :

a. ∠1 is a complement of ∠2, and m∠1 = 62°. Find m∠2.

b. ∠3 is a supplement of ∠4, and m∠4 = 47°. Find m∠3.

Solution

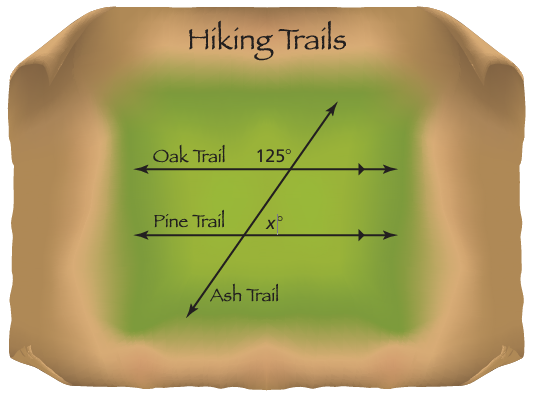
Problem 10 :

What is the value of x?

Solution

Problem 11 :

Find the values of x and y.

Solution

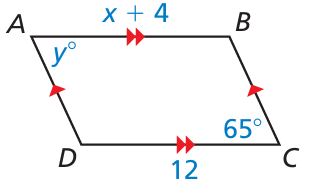
Problem 12 :

Find FG and m∠G.

Solution

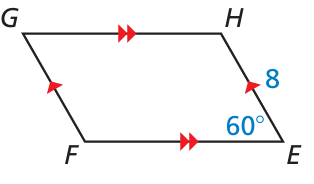
Problem 13 :

Find the values of x and y.

Solution

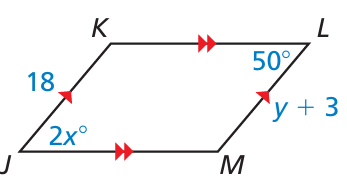
Problem 14 :

For what values of x and y is quadrilateral ABCD a parallelogram? Explain your reasoning.

Solution

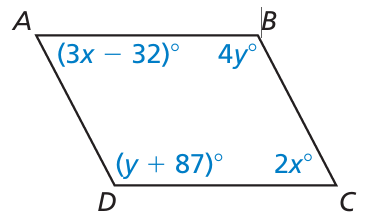
Problem 15 :

You shoot a pool ball, and it rolls back to where it started, as shown in the diagram. The ball bounces off each wall at the same angle at which it hits the wall.

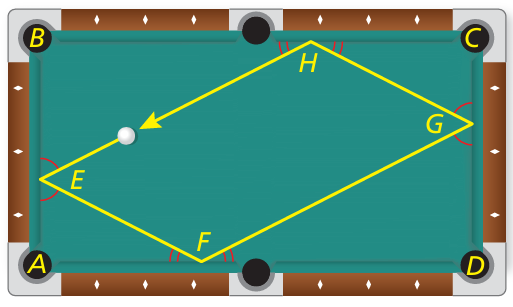
a. The ball hits the first wall at an angle of 63°. So m∠AEF = m∠BEH = 63°. What is m∠AFE? Explain your reasoning.

b. Explain why m∠FGD = 63°.

c. What is m∠GHC? m∠EHB?

d. Is quadrilateral EFGH a parallelogram? Explain your reasoning.

Solution

Problem 1 :

In the parallelogram shown below, find the value of x.

Solution

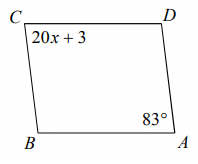
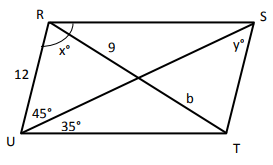
Problem 2 :

Quadrilateral RSTU is a parallelogram. Find the values of x, y, a, and b.

Solution

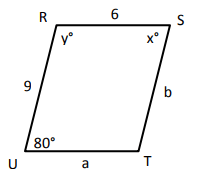
Problem 3 :

Solution

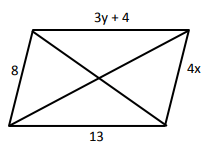
Problem 4 :

Solution

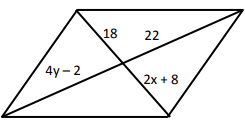
Problem 5 :

Solution

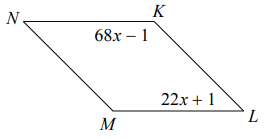
Problem 6 :

Solution

Problem 7 :

Solution

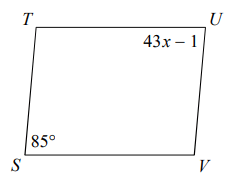
Problem 8 :

Solution

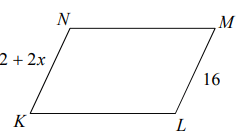
Problem 9 :

Find angle F.

Solution

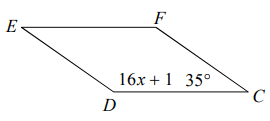
Problem 10 :

Find angle measure R.

Solution

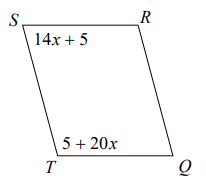
Problem 11 :

In the diagram of the parking lot shown, m∠JKL = 60°, JK = LM = 21 feet, and KL = JM = 9 feet.

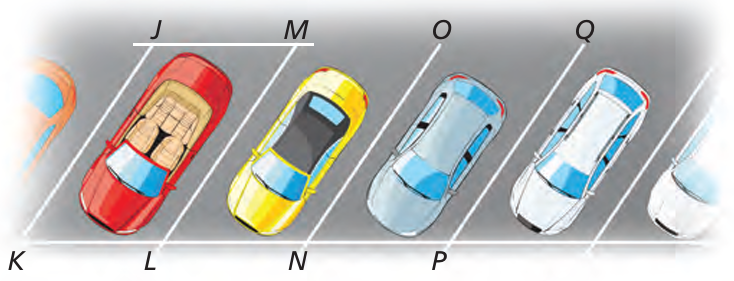
a) Explain how to show that parking space JKLM is a parallelogram.

b) Find m∠JML, m∠KJM, and m∠KLM.

c) LM || NO and NO || PQ . Which theorem could you use to show that JK II PQ ?.

Solution

Problem 12 :

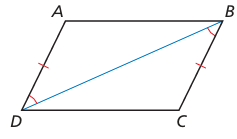
Describe how to prove that ABCD is a parallelogram.

Solution

Problem 13 :

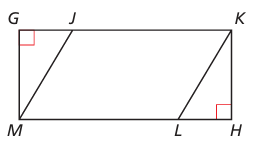
Quadrilateral JKLM is a parallelogram. Describe how to prove that △MGJ ≅ △KHL.

Solution

Problem 14 :

Three interior angle measures of a quadrilateral are 67°, 67°, and 113°. Is this enough information to conclude that the quadrilateral is a parallelogram? Explain your reasoning.

Solution