GEOMETRY PROPERTIES OF PARALLELOGRAMS

Properties of Parallelogram

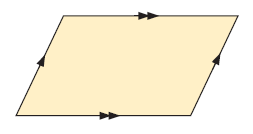
In parallelogram, opposite sides are parallel and equal.

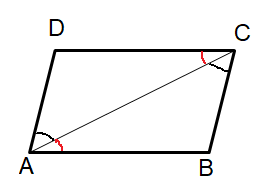
Here diagonal is like a transversal for parallel lines. Then alternate interior angles are equal.

That is, 

∠DAC = ∠ACB, ∠DCA = ∠CAB 

Since the opposite sides are parallel, we observe the same side interior angles.

∠DAB + ∠ADC = 180

∠DCB + ∠CBA = 180

Conclusion :

• Opposite sides are equal
• Opposite angles are equal
• Sum of consecutive interior angles will be 180 degree.
• Diagonals will bisect each other.

Problem 1 :

In the parallelogram shown below, find the value of x.

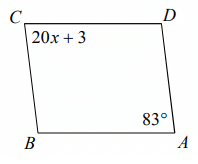
Opposite angles are equal.

20x + 3 = 83

20x = 83 - 3

20x = 80

x = 80/20

x = 4

Problem 2 :

Quadrilateral RSTU is a parallelogram. Find the values of x, y, a, and b.

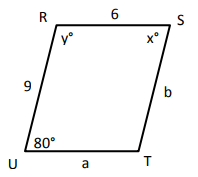
Solution :

Here some angles are missing and some side lengths is also missing.

In parallelogram, opposite sides are equal, opposite angles are equal and consecutive interior angles add upto 180 degree.

80 and y are consecutive interior angles.

80 + y = 180

y = 180 - 80

y = 100

x = 80 (opposite angles)

b = 9 and a = 6

Problem 3 :

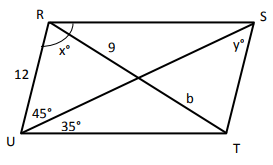
Solution :

y = 35

∠SRU + ∠RUT = 180

x + 45 + 35 = 180

x + 80 = 180

x = 180 - 80

x = 100

Problem 4 :

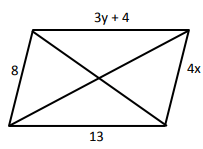
Solution :

Opposite sides are equal.

Problem 5 :

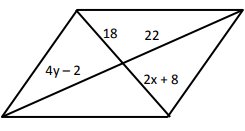
Solution :

Diagonals will bisect each other.

Problem 6 :

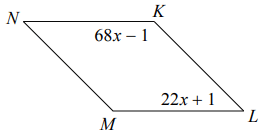
Solution :

Sum of consecutive angles = 180

68x - 1 + 22x + 1 = 180

90x = 180

x = 180 / 90

x = 2

Problem 7 :

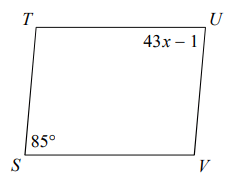
Solution :

∠TUV = ∠TSV

43x - 1 = 85

43x = 85 + 1

43x = 86

x = 86/43

x = 2

Problem 8 :

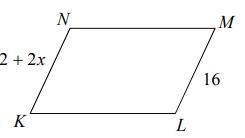
Solution :

MK = ML

2 + 2x = 16

2x = 16 - 2

2x = 14

x = 14/2

x = 7

Problem 9 :

Find angle F.

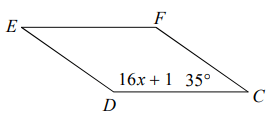
Solution :

Sum of consecutive angles = 180

16x + 1 + 35 = 180

16x + 36 = 180

16x = 180 - 36

16x = 144

x = 144/16

x = 9

∠F + ∠C = 180

∠F + 35 = 180

∠F = 180 - 35

∠F = 145

Problem 10 :

Find angle measure R.

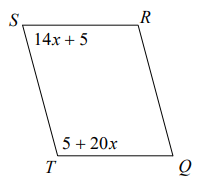
Solution :

Sum of consecutive angles = 180

14x + 5 + 5 + 20x = 180

34x  + 10 = 180

34x = 180 - 10

34x = 170

x = 170/34

x = 5