WORKSHEET ON SOLVING ABSOLUTE VALUE EQUATIONS

Write the solution set of each equation.

Problem 1 :

│x - 5│ = 12

Solution

Problem 2 :

│x + 8│ = 6

Solution

Problem 3 :

│2a - 5│ = 7

Solution

Problem 4 :

│5b - 10│ = 25

Solution

Problem 5 :

│3x - 12│ = 9

Solution

Problem 6 :

│4y + 2│ = 14

Solution

Problem 7 :

│35 - 5x│ = 10 

Solution

Problem 8 :

|-5a│+ 7 = 22

Solution

Problem 9 :

|8 + 2b│ - 3 = 9

Solution

Problem 10 :

│2x - 5│ + 2 = 13

Solution

Problem 11 :

│4x - 12│ + 8 = 0

Solution

Problem 12 :

│7 - x│ + 2 = 12

Solution

Problem 13 :

In a cheerleading competition, the minimum length of a routine is 4 minutes. The maximum length of a routine is 5 minutes. Write an absolute value equation that represents the minimum and maximum lengths

Solution

Problem 14 :

The minimum distance from Earth to the Sun is 91.4 million miles. The maximum distance is 94.5 million miles.

a. Represent these two distances on a number line.

b. Write an absolute value equation that represents the minimum and maximum distances.

Solution

Problem 15 :

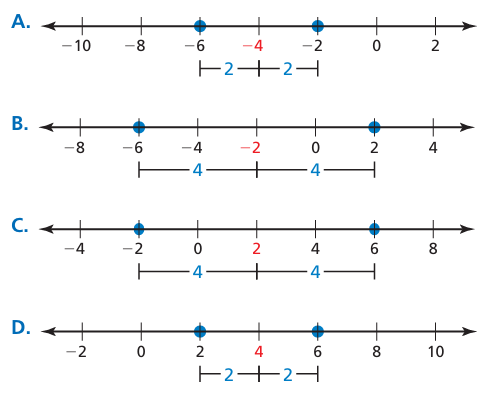
Match the absolute value equation with its graph without solving the equation.

a) ∣ x + 2 ∣ = 4

b) ∣ x − 4 ∣ = 2

c)  ∣ x − 2 ∣ = 4

d) ∣ x + 4 ∣ = 2

Solution

Answer Key

1)  x = 17 (or) x = -7

2)  x = -2 (or) x = -14

3)  a = 6 (or) a = -1

4)  b = 7 (or) b = -3

5) x = 7 (or) x = 1

6)  y = 3 (or) y = -4

7)  x = 5 (or) x = 9

8)  a = -3 (or) a = 3

9)  b = 2 (or) b = -10

10)  x = 8 (or) x = -3

11)  Absolute value cannot be less than 0. So there is no solution.

12)  x = -3 (or) x = 17

13) |x - 4.5| = 0.5

14)  

15)  

a)  Option B

b)  Option D

c)  Option C

d)  Option A

Solve each equation. Check for extraneous solution.

Problem 1 :

|3x – 4| = x              Solution

Problem 2 :

 |x + 24| = -7x         Solution

Problem 3 :

|8x – 1| = 6x               Solution

Problem 4 :

|4x + 5| = 2x + 4        Solution

Problem 5 :

|9 – 2x| = 10 + 3x           Solution

Problem 6 :

 |8 + 5x| = 7 - x           Solution

Solve each equation. Check for extraneous solution.

Problem 1 :

|x – 1| = 5x + 10

Solution

Problem 2 :

|2z – 3| = 4z - 1

Solution

Problem 3 :

|3x + 5| = 5x + 2

Solution

Problem 4 :

|2y – 4| = 12

Solution

Problem 5 :

3|4w – 1| - 5 = 10

Solution

Problem 6 :

|2x + 5| = 3x + 4

Solution

Solve for x :

Problem 1 :

|(3x + 2)/(1 – x)| = 4

Solution

Problem 2 :

|x /(x – 1)| = 3

Solution

Problem 3 :

|(2x - 1)/(x + 1)| = 5

Solution

Problem 4 :

|(x + 3)/(1 – 3x)| = 1/2

Solution

Problem 5 :

|x/(x – 2)| = 3

Solution

Problem 6 :

|(2x + 3)/(x – 1)| = 2

Solution

Problem 1 :

|x + 3| = 2

Solution

Problem 2 :

|x - 3| = 1

Solution

Problem 3 :

|x + 1| = 1

Solution

Problem 4 :

|1 + x| = 3

Solution

Problem 5 :

3|x – 2| + 3 = 6

Solution

Problem 6 :

3 - 4|x - 1| = -1

Solution

Problem 7 :

4 + |x + 1| = 5

Solution

Problem 8 :

2|x + 2| + 3 = 5

Solution