ABSOLUTE VALUE EQUATION WITH EXTRANEOUS SOLUTION

Extraneous solutions are values that we get when solving equations that aren't really solutions to the equation.

To find extraneous solution for absolute value function, we follow the steps given below.

(i) Decompose the absolute function in the form of 

Absolute sign on one side

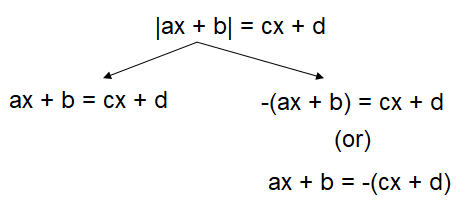
Absolute sign on both sides

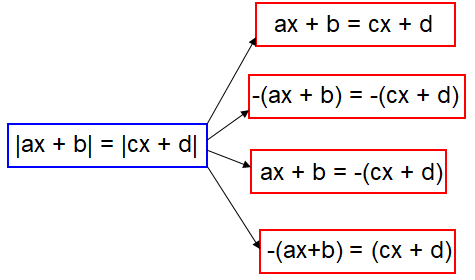
Note :

In the branches, first two are the same and last two are the same.

(ii)  Apply the values that we have received into the original question and check which value satisfies the equation of not.

The values that doesn't satisfy the equation is known as extraneous solution.

Solve each equation. Check for extraneous solution.

Problem 1 :

|3x – 4| = x

Solution :

|3x – 4| = x

3x – 4 = x

3x – x = 4

2x = 4

x = 2

3x – 4 = -x

3x + x = 4

4x = 4

x = 1

Checking extraneous solution :

If x = 2

|3x – 4| = x

|3(2) – 4| = 2

|6 – 4| = 2

2 = 2

If x = 1

|3x – 4| = x

|3(1) – 4| = 1

|3 – 4| = 1

1 = 1

Both values are satisfying the function, so there is no extraneous solution.

Problem 2 :

|x + 24| = -7x

Solution :

|x + 24| = -7x

x + 24 = -7x

x + 7x = -24

8x = -24

x = -3

x + 24 = 7x

x - 7x = -24

-6x = -24

x = 4

Checking extraneous solution :

If x = -3

|x + 24| = -7x

|(-3) + 24| = -7(-3)

|21| = 21

21 = 21

If x = 4

|x + 24| = -7x

|4 + 24| = -7(4)

|28| = -28

28 ≠ -28

So, 4 is extraneous solution.

Problem 3 :

|8x – 1| = 6x

Solution : 

|8x – 1| = 6x

8x – 1 = 6x

8x – 6x = 1

2x = 1

x = 1/2

8x – 1 = -6x

8x + 6x = 1

14x = 1

x = 1/14

Checking extraneous solution :

If x = 1/2

|8x – 1| = 6x

|8(1/2) – 1| = 6(1/2)

|3| = 3

3 = 3

If x = 1/14

|8x – 1| = 6x

|8(1/14) – 1| = 6(1/14)

|8/14 – 1| = 6/14

6/14 = 6/14

So, there is no extraneous solution.

Problem 4 :

|4x + 5| = 2x + 4

Solution:

|4x + 5| = 2x + 4

4x + 5 = 2x + 4

4x – 2x = 4 – 5

2x = -1

x = -1/2

4x + 5 = -2x – 4

4x + 2x = -4 – 5

6x = -9

x = -3/2

Checking extraneous solution :

If x = -1/2

|4x + 5| = 2x + 4

|4(-1/2) + 5| = 2(-1/2) + 4

|-2 + 5| = -1 + 4

|3| = 3

3 = 3

If x = -3/2

|4x + 5| = 2x + 4

|4(-3/2) + 5| = 2(-3/2) + 4

|-6 + 5| = |-3 + 4|

|-1| = 1

1 = 1

Both values are satisfying the absolute value equation, so there is no extraneous solution.

Problem 5 :

|9 – 2x| = 10 + 3x

Solution :

|9 – 2x| = 10 + 3x

9 – 2x = 10 + 3x

9 – 10 = 3x + 2x

-1 = 5x

-1/5 = x

9 – 2x = -10 - 3x

9 + 10 = -3x + 2x

19 = -x

-19 = x

Check for extraneous solution :

If x = -1/5

|9 – 2x| = 10 + 3x

|9 – 2(-1/5)| = 10 + 3(-1/5)

|9 + 2/5| = 10 – 3/5

|47/5| = 47/5

47/5 = 47/5

If x = -19

|9 – 2x| = 10 + 3x

|9 – 2(-19)| = 10 + 3(-19)

|9 + 38| = 10 – 57

|47| = -47

47 ≠ -47

So, -19 is a extraneous solution.

Problem 6 :

|8 + 5x| = 7 - x

Solution :

Given, |8 + 5x| = 7 – x

8 + 5x = 7 – x

5x + x = 7 – 8

6x = -1

x = -1/6

8 + 5x = -7 + x

5x – x = -7 – 8

4x = -15

x = -15/4

Check for extraneous solution :

If x = -1/6

|8 + 5x| = 7 – x

|8 + 5(-1/6)| = 7 – (-1/6)

|8 – 5/6| = 7 + 1/6

|(48 – 5)/6| = (42 + 1)/6

|43/6| = 43/6

43/6 = 43/6

If x = -15/4

|8 + 5x| = 7 – x

|8 + 5(-15/4)| = 7 – (-15/4)

|8 - 75/4| = 7 + 15/4

|(32 – 75)/4| = (28 + 15)/4

|-43/4| = 43/4

So, there is no extraneous solution.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More