VERTICALLY OPPOSITE ANGLES WORKSHEET

Find the unknown angles in the following figures.

Problem 1 :

Solution

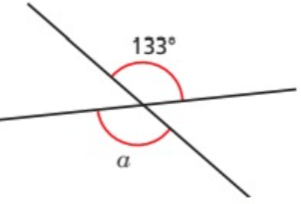
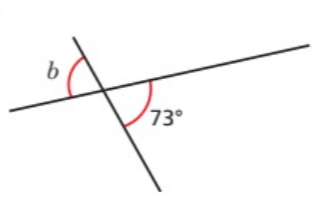
Problem 2 :

Solution

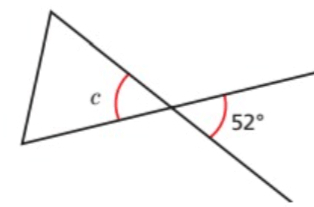
Problem 3 :

Solution

Problem 4 :

Solution

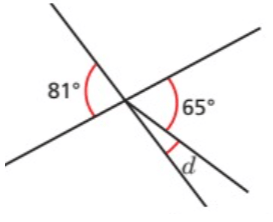
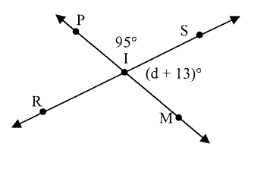
Problem 5 :

Find the value of m.

Solution

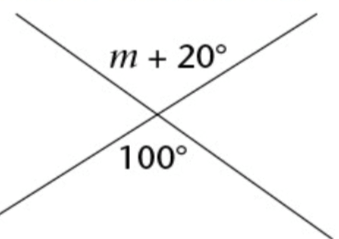
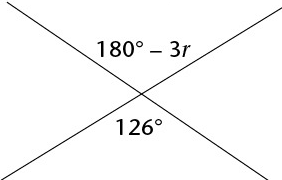
Problem 6 :

Solution

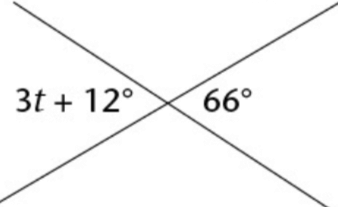
Problem 7 :

Find the value of p.

Solution

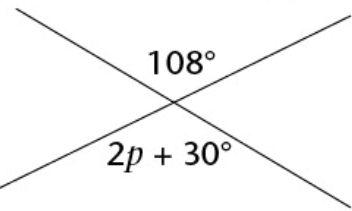
Problem 8 :

Find the value of z.

Solution

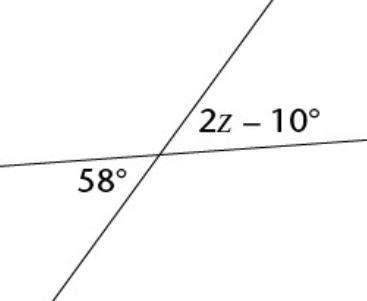
Problem 9 :

Find the value of y.

Solution

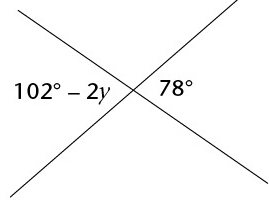
Problem 10 :

Find the value of r.

Solution

Problem 1 :

Angles A and B are complementary. If m∠A = 3x - 8 and m∠B = 5x + 10, what is the measure of each angle ?

Solution

Problem 2 :

Angles Q and R are supplementary. If m∠Q = 4x + 9 and m∠R = 8x + 3, what is the measure of each angle ?

Solution

Problem 3 :

Find the measure of two complementary angles ∠A and ∠B, if m∠A = 7x + 4 and m∠B = 4x+ 9.

Solution

Problem 4 :

The measure of an angle is 44 more than the measure of its supplement. Find the measures of the angles.

Solution

Problem 5 :

What are the measures of two complementary angles if the difference in the measures of the two angles is 12.

Solution

Problem 6 :

Find the measures of two supplementary angles ∠N and ∠M if the measure of angle N is 5 less than 4 times the measure of angle M.

Solution

Problem 7 :

Suppose ∠T and ∠U are complementary angles. Find x, if ∠T = 16x - 9 and ∠U = 4x - 1.

Solution

Problem 8 :

Two angles are vertical in relation. One angle is 2y and the other angle is y + 130. Find each angle measure.

Solution

Problem 9 :

The measure of two supplementary angles are in the ratio 4 : 2, Find those two angles.

Solution

Problem 1 :

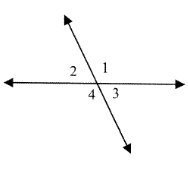
From the picture at the right, name the 4 sets of linear pair angles?

Solution

Problem 2 :

From the picture at the right, name the 2 sets of vertical angles?

Solution

Problem 3 :

Vertical angles are always ________.

Solution

Problem 4 :

Linear pairs are always _____, which means they add up to _____.

Solution

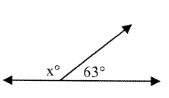
Problem 5 :

x = _____

Problem 6 :

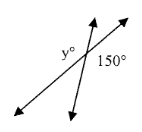
y = _____

Solution

Problem 7 :

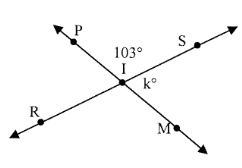
k = _____

Solution

Problem 8 :

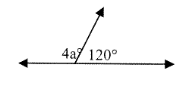
a = _____

Solution

Problem 9 :

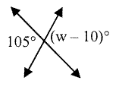
w = _____

Solution

Problem 10 :

d = _____

Tell whether the statement is always, sometimes, or never true. Explain your reasoning.

Problem 11 :

Complementary angles are adjacent.

Solution

Problem 12 :

Angles in a linear pair are supplements of each other.

Solution

Problem 13 :

Vertical angles are adjacent.

Solution

Problem 14 :

Vertical angles are supplements of each other.

Solution

Problem 15 :

If an angle is acute, then its complement is greater than its supplement.

Solution

Problem 16 :

If two complementary angles are congruent, then the measure of each angle is 45°. 

Solution

Problem 17 :

Explain why the supplement of an acute angle must be obtuse. 

Solution

Problem 18 :

Explain why an obtuse angle does not have a complement.

Solution

Problem 19 :

The iron cross is a skiing trick in which the tips of the skis are crossed while the skier is airborne. Find the value of x in the iron cross shown.

Solution

Write and solve an algebraic equation to find the measure of each angle based on the given description.

Problem 20 :

The measure of an angle is 9 more than twice its complement. 

Solution

Problem 21 :

Two angles form a linear pair. The measure of one angle is four times the measure of the other angle.

Solution