PROBLEMS ON VERTICALLY OPPOSITE ANGLES

Vertically opposite angles are equal in size.

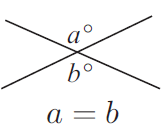
Find the unknown angles in the following figures.

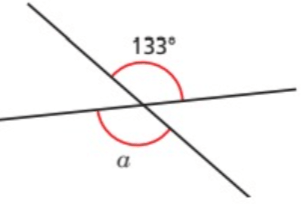
Problem 1 :

Solution :

Since a and 133 are vertically opposite, they will be equal.

So, ∠a = 133.

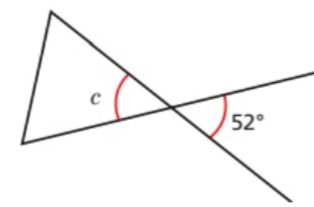
Problem 2 :

Solution :

Since c and 52 are vertically opposite, they will be equal.

So, ∠c = 52

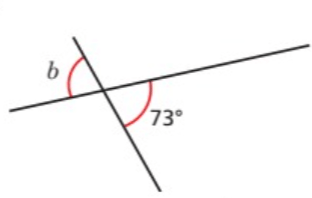
Problem 3 :

Solution :

Since b and 73 are vertically opposite, they will be equal.

So, ∠b = 73

Problem 4 :

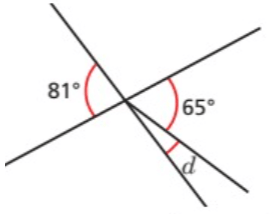
Solution :

81 = 65 + d

Subtracting 65 on both sides, we get

81 - 65 = d

d = 16

Problem 5 :

Find the value of m.

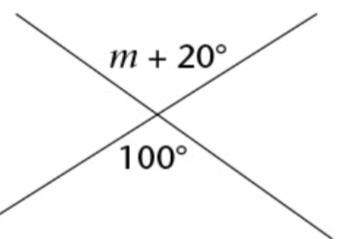
Solution :

m + 20 = 100

Subtracting 20 on both sides.

m = 100 - 20

m = 80

Problem 6 :

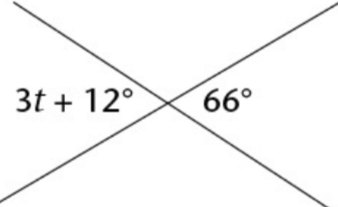
Solution :

3t + 12 = 66

Subtracting 12 on both sides.

3t = 66 - 12

3t = 54

Dividing by 3, we get

t = 54/3

t = 18

Problem 7 :

Find the value of p.

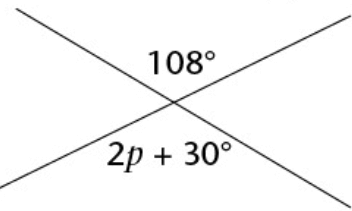
Solution :

2p + 30 = 108

Subtracting 30 on both sides.

2p = 108 - 30

2p = 78

Dividing by 2, we get

p = 78/2

p = 39

Problem 8 :

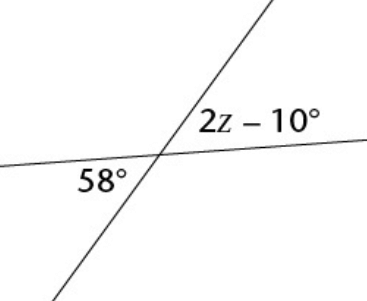
Find the value of z.

Solution :

58 and 2z - 10 are vertically opposite angles.

58 = 2z - 10

Add 10 on both sides.

68 = 2z

dividing by 2

z = 68/2

z = 34

Problem 9 :

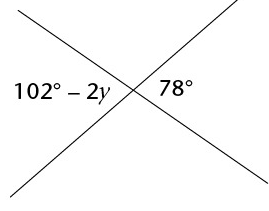
Find the value of y.

Solution :

102 - 2y and 78 are vertically opposite angles.

78 = 102 - 2y

Add 2y on both sides.

2y + 78 = 102

Subtracting 78, we get

2y = 102 - 78

2y = 24

Dividing by 2 on both sides.

y = 24/2

y = 12

Problem 10 :

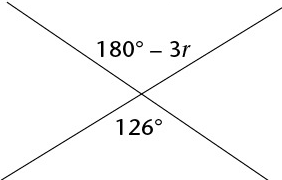
Find the value of r.

Solution :

126 and 180 - 3r are vertically opposite angles.

126 = 180 - 3r

Add 3r on both sides.

126 + 3r = 180

Subtracting 126 on both sides.

3r = 180 - 126

3r = 54

r = 54/3

r = 18