SOLVING WORD PROBLEMS USING PYTHAGOREAN THEOREM WORKSHEET

Problem 1 :

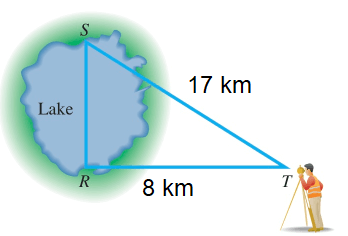
A land surveyor uses this diagram to find x, find the length of lake.

Solution

Problem 2 :

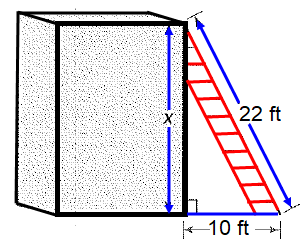
A foot ladder leans against a shed reaching a height of x feet. The base of the ladder is 10 feet from the shed.

Solution

Problem 3 :

The diagram shows a sailboat. What is approximate area of the sail shown ?

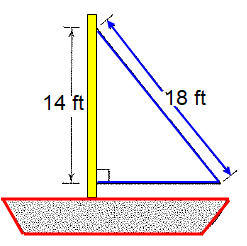
(a)  79 square feet     (b)  126 square feet

(c)  158 square feet      (d)  200 square feet

Solution

Problem 4 :

The television screen has a 25 inch diagonal and a 15 inch height. What is the area of the screen ?

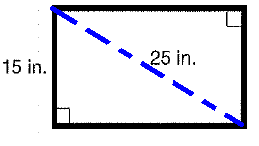
(a)  150 square inches    (b)  300 square inches

(c)  375 square inches   (d) 437 square inches

Solution

Problem 5 :

If two forces, A and B pull at right angles from each other, the resultant force can be represented as the diagonal of a rectangle.

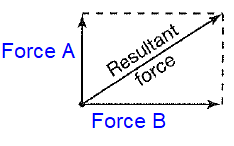
If a 21 pound force and a 28 pound force are pulling of an object, and the resultant force is 35 pounds, are the forces pulling a right angles ?

Solution

Problem 6 :

The distance across a pond cannot be directly measured. A land surveyor takes some other measurements and uses them to find d, the distance across the pond.

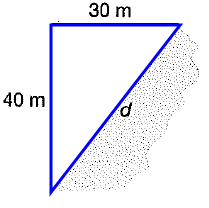
What is the distance across the pond ?

(a)  70 meters   (b) 35 meters   (c)  50 meters    (d) 10 meters

Solution

Problem 7 :

The solid line below show the route Maddy's bus takes to school. The dashed line shows a shortcut she takes through the park when she rides her bike to school. What is the difference in km between the shortcut and the usual route ?

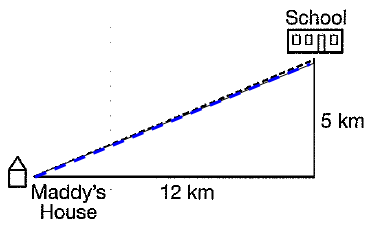
(a)  10 km     (b)  4 km     (c)  7 km    (d)  3 km

Solution

Problem 8 :

On the map below, the post office is at origin (0, 0) and each unit represents 1 km. Amy lives 6 km east and 8 km north of the post office. if she rides her bike directly from her house to the post office, how far will she ride her bike ?

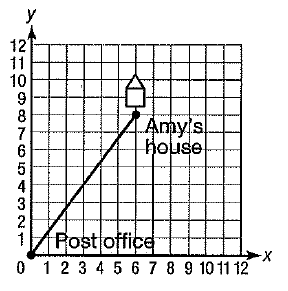
(a)  4.8 km   (b)  12 km   (c)  10 km   (d)  14 km

Solution

For each triangle find the missing length. Round your answer to the nearest tenth. Then find the area and the perimeter.

Problem 1 :

Solution

Problem 2 :

Solution

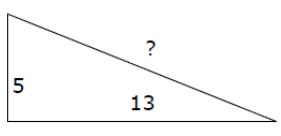
Problem 3 :

Find a third number so that the three numbers form a right triangle:

i) 9 , 41

Solution

Problem 4 :

Ms. Green tells you that a right triangle has a hypotenuse of 13 and a leg of 5. She asks you to find the other leg of the triangle. What is your answer?

Solution

Problem 5 :

Thes sides of a triangle have lengths x, x + 5, and 25. If the length of the longest side is 25, what value of x makes the triangle a right triangle?

Solution

Problem 6 :

A 22 foot ladder lean against a shed reaching a height of x feet. The base of the ladder is 10 feet from the shed.

Solution

Problem 7 :

A small shelf sits on two braces that are in the shape of a right triangle. The leg (brace) attached to the wall is 4.5 inches and the hypotenuse is 7.5 inches. The leg holding the shelf is the same length as the width of the shelf. What is the width of the shelf?

Solution

Problem 8 :

Can a right triangle have a leg that is 10 meters long and a hypotenuse that is 10 meters long? Explain.

Solution

Problem 9 :

One leg of a right triangular piece of land has a length of 24 yards. The hypotenuse has a length of 74 yards. The other leg has a length of 10x yards. What is the value of x?

Solution

Problem 10 :

You built braces in the shape of a right triangle to hold your surfboard. The leg (brace) attached to the wall is 10 inches and your surfboard sits on a leg that is 24 inches. What is the length of the hypotenuse that completes the right triangle?

Solution

Problem 11 :

Laptops are advertised by the lengths of the diagonals of the screen. You purchase a 15-inch laptop and the width of the screen is 12 inches. What is the height of its screen?

Solution

Problem 12 :

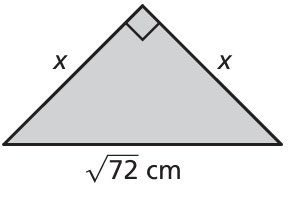
In a right isosceles triangle, the lengths of both legs are equal. For the given isosceles triangle, what is the value of x?

Solution