FIND THE MISSING SIDE LENGTH USING PYTHAGOREAN THEOREM

For each triangle find the missing length. Round your answer to the nearest tenth. Then find the area and the perimeter.

Problem 1 :

Solution :

Let the missing side be x.

hypotenuse = 19

x² + 17² = 19²

x² + 289 = 361

x² = 361 - 289

x² = 72

x = √72

x = 8.48

Problem 2 :

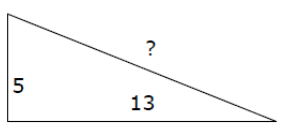
Solution :

Let the missing side be x.

hypotenuse = x

5² + 13² = x²

25 + 169 = x²

x² = 194

x = √194

x = 13.92

Problem 3 :

Find a third number so that the three numbers form a right triangle:

i) 9 , 41

Solution :

Let x be the unknown.

In the given measure 41 is the greatest.

41² = 9² + x²

1681 = 81 + x²

Subtracting 81 on both sides.

1681 - 81 = x²

x² = 1600

x = √1600

x = 40

Problem 4 :

Ms. Green tells you that a right triangle has a hypotenuse of 13 and a leg of 5. She asks you to find the other leg of the triangle. What is your answer?

Solution :

Hypotenuse = 13, one leg = 5, other leg = x ?

x² + 5² = 13²

x² + 25 = 169

x² = 169 - 25

x² = 144

x = √144

x = 12

Problem 5 :

Thes sides of a triangle have lengths x, x + 5, and 25. If the length of the longest side is 25, what value of x makes the triangle a right triangle?

Solution :

Longest side = 25

25² = x² + (x + 5)²

625 = x² + x² + 2x(5) + 5²

625 = 2x² + 10x + 25

2x² + 10x + 25 - 625 = 0

2x² + 10x - 600 = 0

Dividing by 2, we get

x² + 5x - 300 = 0

(x - 15)(x + 20) = 0

x = 15 and x = -20

Since x is one of the side of the triangle, we ignore -20.

So, the value of x is 15.

Problem 6 :

A 22 foot ladder lean against a shed reaching a height of x feet. The base of the ladder is 10 feet from the shed.

Solution :

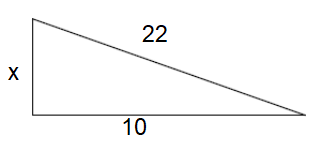
22² = x² + 10²

484 = x² + 100

x² = 484 - 100

x² = 384

x = √384

x = 19.59

Approximately height of the wall is 19.6 feet. 

Problem 7 :

A small shelf sits on two braces that are in the shape of a right triangle. The leg (brace) attached to the wall is 4.5 inches and the hypotenuse is 7.5 inches. The leg holding the shelf is the same length as the width of the shelf. What is the width of the shelf?

Solution :

Hypotenuse = 7.5 inches

Measure of one leg = 4.5 inches

Let x be the measure of other leg.

7.5² = x² + 4.5²

56.25 = x² + 20.25

x² = 56.25 - 20.25

x² = 36

x = √36

x = 6

So, the width of the shelf is 6 inches.

Problem 8 :

Can a right triangle have a leg that is 10 meters long and a hypotenuse that is 10 meters long? Explain.

Solution :

Given that length of one leg = 10 m and hypotenuse = 10 m

In any right triangle, hypotensue will be the longest side. When one of the sides measures 10 meter, then hypotenuse should be greater than 10 meter. So, for the given situation, we cannot create a right triangle.

Problem 9 :

One leg of a right triangular piece of land has a length of 24 yards. The hypotenuse has a length of 74 yards. The other leg has a length of 10x yards. What is the value of x?

Solution :

Measure of one leg = 24 yards, other leg = 10x yards

Hypotenuse = 74 yards

Using Pythagorean theorem, 

24² + (10x)² = 74²

576 + 100 x² = 5476

100 x² = 5476 - 576

100 x² = 4900

x² = 4900/100

x² = 49

x = 7

So, the value of x is 7 yards.

Problem 10 :

You built braces in the shape of a right triangle to hold your surfboard. The leg (brace) attached to the wall is 10 inches and your surfboard sits on a leg that is 24 inches. What is the length of the hypotenuse that completes the right triangle?

Solution :

Measures of legs are 10 inches and 24 inches

Let x be the length of hypotenuse

Using Pythagorean theorem,

x² = 10² + 24²

x² = 100 + 576

x² = 676

x = √676

x = 26 inches

So, hypotenuse of the triangle is 26 inches.

Problem 11 :

Laptops are advertised by the lengths of the diagonals of the screen. You purchase a 15-inch laptop and the width of the screen is 12 inches. What is the height of its screen?

Solution :

Let x be the height of the triangle.

Diagonal = 15 inch, width = 12 inch

15² = 12² + x²

225 = 144 + x²

x² = 225 - 144

x² = 81

x = √81

x = 9 inches

So, the height of the screen is 9 inches.

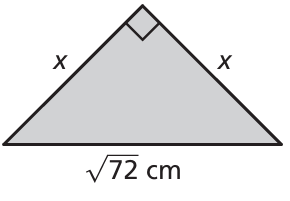
Problem 12 :

In a right isosceles triangle, the lengths of both legs are equal. For the given isosceles triangle, what is the value of x?

Solution :

Using Pythagorean theorem, 

√72² = x² + x²

2x² = 72

x² = 72/2

x² = 36

x = √36

x = 6

So, the measure of x is 6 cm.