RELATIONS AND FUNCTION PRACTICE WORKSHEET ALGEBRA 2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Given the relation R = {(-2, 3) (a, 4) (1, 9) (0, 7)} which replacement for a makes this relation a function ?
a) 1 b) -2 c) 0 d) 4
Problem 2 :
Which relation is not a function ?
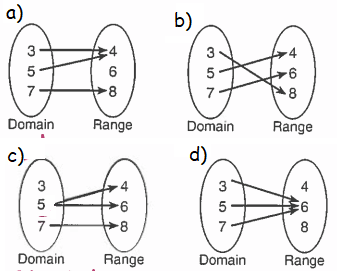
Problem 3 :
If f(x) = x2 - 2x + 3, find the value of f(-2)
Problem 4 :
If f(x) = (x - 2) / (x + 1), then the value of f(n + 1) is equal to
Problem 5 :
If f(x) = 4x2 - x + 1, then f(a + 1) = ?
Problem 6 :
If f(x) = x2 - 3x, find f(x/2)
Problem 7 :
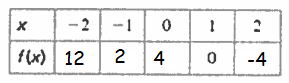
1) Find the following values of the function.
i) f(2) = ii) f(0) =
2) For which of the values of x is this statement true ?
f(x) = 2
Problem 8 :
If the domain of f(x) = 2x + 3 is {-1, 0, 2} which number is not in range ?
a) 1 b) 2 c) 3 d) 7
Problem 9 :
The function is defined by the equation y = 8x - 3. If the domain is 2 ≤ x ≤ 4, find the minimum value in the range, find the minimum value in the range of the function.
Problem 10 :
Find the inverse of the following function
{(2, 6) (-3, 4) (-7, -5)}
The minimum value in the range is 13.
Problem 11 :
Find the inverse of the function
y = 3x + 2
Problem 12 :
In which of the following graphs
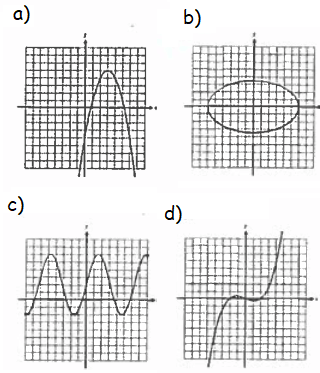
Problem 13 :
Which graph is not a function.
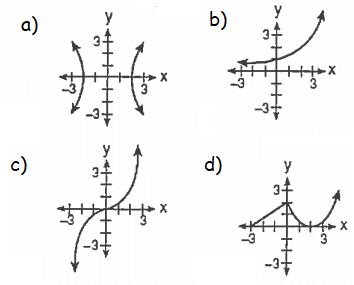
Problem 14 :
Which graph represents one to one function
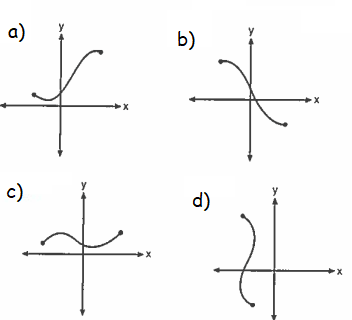
Answer Key
1) a = 4
2) option c
3) f(-2) is 11.
4) f(n + 1) = (n - 1)/(n + 2)
5) 4a2 + 7a + 4
6) x2/4 - 3x/2
7) 1) i) f(2) = -4 ii) f(0) = 4
2) f(-1) = 2
8) Range = {1, 3, 7}
9) range is 13.
10) f-1(x) = {(6, 2) (4, -3) (-5, -7)}
11) y = (x/3) - (2/3)
12) option b
13) option a
14) option b
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling